Задача 69651 Если a+b+c=0 и |a| = |b|=|c|=a,то...

637a67e77f38ed72902f90f8

27.02.2023 20:59:17

Если a+b+c=0 и |a| = |b|=|c|=a,то а*b+a*c+b*c найдите значения выражения

626fab9a354ab65fb2f43abb

27.02.2023 22:07:17

★

Здесь речь идет о векторах.
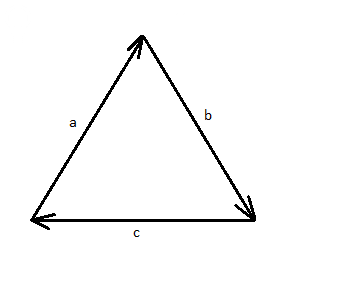
Если a + b + c = 0 и |a| = |b| = |c| = a, то эти три вектора образуют равносторонний треугольник со стороной а.
Он показан на рисунке.
Углы между векторами:
(a; b) = (b; c) = (c; a) = 60° = π/3
Скалярные произведения:
a*b = |a|*|b|*cos π/3 = a*a*1/2 = a^2/2
b*c = |b|*|c|*cos π/3 = a*a*1/2 = a^2/2
c*a = |c|*|a|*cos π/3 = a*a*1/2 = a^2/2
Сумма:
a*b + b*c + c*a = a^2/2 + a^2/2 + a^2/2 = 3a^2/2