Задача 68967 Решите ???????? ...
Условие
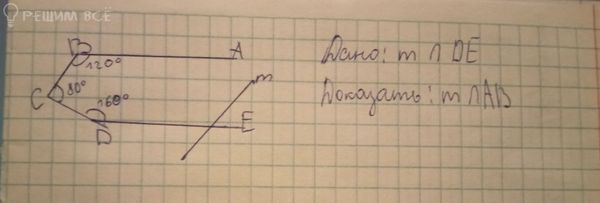
6-7 класс
209
Решение
★
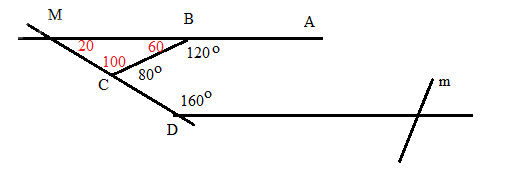
В ΔМСВ получаем:
∠СВМ=180^(o)-120^(o)=60^(o) - как угол, смежный с ∠СВА,
∠МСВ=180^(o)-80^(o)=100^(o) - как угол, смежный с ∠ВСD,
∠СМВ=180^(o)-( ∠CВМ+ ∠МСВ)=180^(o)-(60^(o)+100^(o))=20^(o).
∠ВМD и ∠СDE- односторонние углы при прямых АВ и DE и секущей МD.
∠ВМD + ∠СDE=20^(o)+160^(o)=180^(o).
Так как сумма односторонних углов равна 180^(o), то прямые АВ и DE параллельны.
Прямая m пересекает прямую DE. А если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую прямую, значит, m пересекает АВ, что и требовалось доказать.