Задача 689 В цилиндрическом сосуде уровень жидкости...
Условие
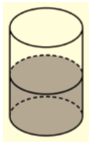
Решение
PiR^2*16 = Pi(2R)^2*h
h=16/4=4
Ответ: 4
Решение
Неоригинально обозначим радиус первого цилиндра буквой R. Ясно, что радиус второго при таких обстоятельствах получается = 2R.
Тогда объем жидкости в первом цилиндре - произведение площади круга (основания этого цилиндра) на высоту столбика
Пи х R^2 х 16
Высота столбика жидкости во втором цилиндре получится, если поделить тот же объем жидкости на площадь его (второго цилиндра) основания. Назовем ее Н:
Н = (Пи х R^2 х 16)/(Пи х (2R)^2) = (Пи х R^2 х 16)/(Пи х 4 х R^2) = 16/4
Вот как интуиция подвела на этот раз!)
Оказалось, зависимость тут не прямая, а квадратичная - если диаметр меняется вдвое, высота столба жидкости меняется в 2^2 = вчетверо!