Задача 6883 4cos^3(x/2)+3sqrt(2)sinx(x) =...
Условие
Как решить данное уравнение?
математика 10-11 класс
5505
Решение
★
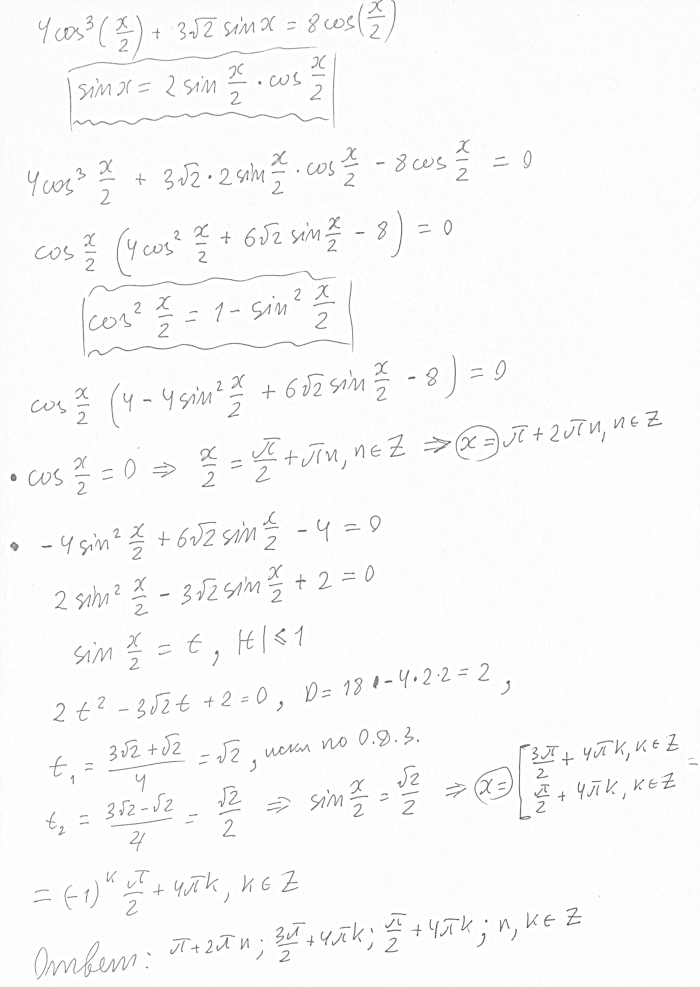
Все решения
4cos^3(x/2) + 6sqrt(2)sin(x/2)cos(x\2) - 8cos(x/2) = 0. Делим на 2 и выносим за скобки cos(x/2):
cos(x/2) * (2cos^2(x\2) - 4 + 3sqrt(2)sin(x/2) ) = 0.
cos(x/2) =0 (т.е. x = пи +2*пи*k) или скобка.В скобке: заменяем cos^2 на sin^2:
2 - 2sin^2(x/2) - 4 + 3sqrt(2)sin(x/2) = 0. Заменяем sin(x/2) на t:
2*t^2 - 3sqrt(2)*t + 2 = 0
D = 2, sqrt(D) = sqrt(2).
t1 = 2sqrt(2), t2 = sqrt(2)
Но так как t = sin(x/2), то таких ответов не может быть. Остается только один.
Ответ: x = пи +2*пи*k