Задача 688 На рисунке изображён график...

slava191

27.02.2014

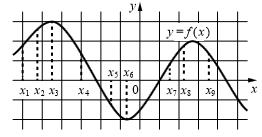
На рисунке изображён график дифференцируемой функции y=f(x). На оси абсцисс отмечены девять точек: x1 ,x2 , ...,x9 . Среди этих точек найдите все точки, в которых производная функции f(x) отрицательна. В ответе укажите количество найденных точек.

Значение производной в своём геометрическом смысле есть тангенс (кэфициент) угла наклона касательной. Такой коэффициент отрицательный когда касательная к графику функции стремится вниз.

В данном случае это точки : x4, x5, x9 и всего их 3

Ответ: 3

Ответ: 3

Гость

15.09.2014

4