Задача 68342 Две машины движутся по двум взаимно...
Условие
прямолинейным дорогам по направлению к перекрестку с постоянными
скоростями 50 км/ч и 100 км/ч.
В начальный момент времени первая машина находилась на расстоянии 200 м от перекрестка, а вторая на расстоянии 300 м.
Через сколько времени расстояние между ними будет минимальным?
Решение
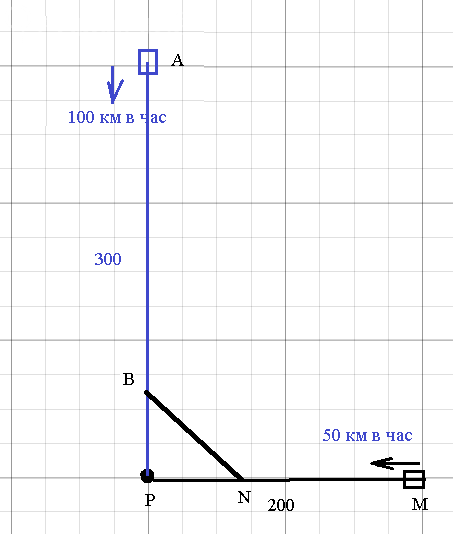
BP=300-100t
MN=50t
NP=200-50t
BN^2=BP^2+PN^2=(300-100t)^2+(200-50t)^2
функцию
f(t)=(300-100t)^2+(200-50t)^2
Исследовать функцию на наименьшее значение
Это квадратичная функция.
Наименьшее значение в вершине параболы
Упрощаем
f(t)=100^2*(3-t)^2+50^2*(4-t)^2
f(t)=50^2*(4*(9-6t+t^2)+16-8t+t^2)
f(t)=50^2*(36-24t+4t^2+16-8t+t^2)
f(t)=50^2*(52-32t+5t^2)
t_(o)=32/10=3,2
Это значит автомобиль проедет за перекресток.
Потому как до точки Р ему ехать 300:100=3 часа.