Задача 68264 ...

639f425f46194a06fd2f2f08

12.01.2023 18:41:24

Радиус круга описанного вокруг основы призмы равен R. Каждое боковое ребро пирамиды образует с площадью ее основы угол α . Найдите радиус шара описанной вокруг данной пирамиды

5f3ea7e3faf909182968ddd9

12.01.2023 20:07:53

★

В основании квадрат ⇒ диагональ квадрата = диаметру круга

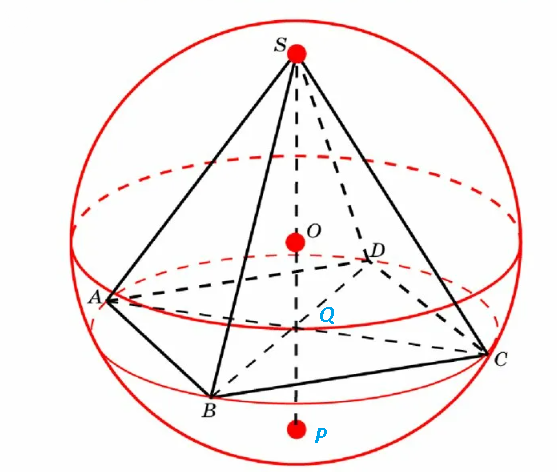
AC=BD=2R

Каждое боковое ребро пирамиды образует с площадью ее основы угол α

⇒

H_(пирамиды)=[b]R*tg α [/b]


Обозначим радиус шара [b]х[/b]:

SO=OP=x

SP=2x

SQ=H_(пирамиды)=[b]R*tg α [/b]



По свойству пересекающихся хорд

AQ*QC=AQ*QP


R*R=(2x-H)*H ⇒ R^2=(2x-R*tg α)*R*tg α ⇒ 2xRtg α -R^2tg^2 α =R^2
2xRtg α=R^2(tg^2 α+1)

2xtg α=R*(tg^2 α+1)


1+tg^2 α =1/cos^2 α

2x*sin α/cos α =R(1/cos^2 α )

x*2sin α*cos α =R

[b]x=R/sin2 α [/b]