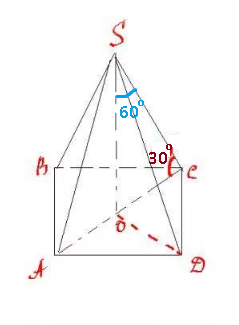
Задача 68240 Боковое ребро правильной четырехугольной...

639f425f46194a06fd2f2f08

12.01.2023 00:03:05

Боковое ребро правильной четырехугольной пирамиды равно 6см и образует угол 60° с высотой пирамиды. Найдите площадь осевого сечения конуса, описанного вокруг этой пирамиды

5f3ea7e3faf909182968ddd9

12.01.2023 00:19:55

★

Δ SOC - прямоугольный с острыми углами 60 ° и 30 °

Катет против угла в 30 ° равен половине гипотенузы

SO=3 см

OC=sqrt(6^2-3^2)=sqrt(27)=3sqrt(3)

ABCD - квадрат

Радиус окружности, описанной около квадрата

R=OC

S_(осевого сечения конуса)=S_( Δ SAC)=(1/2)AC*SO=3sqrt(3)*3=9sqrt(3)