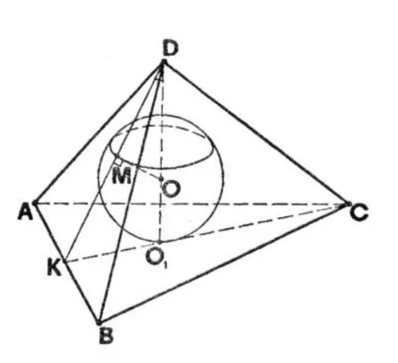
Задача 68214 Сторона основания правильной треугольной...

639f425f46194a06fd2f2f08

10.01.2023 22:50:11

Сторона основания правильной треугольной пирамиды равна 24 sqrt(3 )см, а центр шара, вписанного в пирамиду, делит ее высоту в отношении 5:4, двигая от вершины пирамиды. Найдите высоту пирамиды.

5f3ea7e3faf909182968ddd9

11.01.2023 00:05:57

★

СК=asqrt(3)/2=24sqrt(3)*sqrt(3)/2=36

CO_(1):O_(1)K=2:1

CO_(1)=24
O_(1)K=12

DO:OO_(1)=5:4

DO=5x
OO_(1)=r=4x

DO_(1)=DO+OO_(1)=5x+4x=[b]9x[/b]

OM=r=4x

KM=KO_(1)=12

ΔDMO и Δ DO_(1)K - прямоугольные
∠ DMO= ∠ DO_(1)K=90 °


По теореме Пиафгора из ΔDMO

DM^2=DO^2-MO^2=(5x)^2-(4x)^2=9x^2

DM=3x
По теореме Пифfгора изΔ DO_(1)K:

DK^2=DO^2_(1)+O_(1)K^2

DK=DM+MK=3x+12

(3x+12)^2=(9x)^2+12^2

х=

DO_(1)=[b]9x[/b]=