Задача 67950 Вычислить производную сложной функции ...
Условие
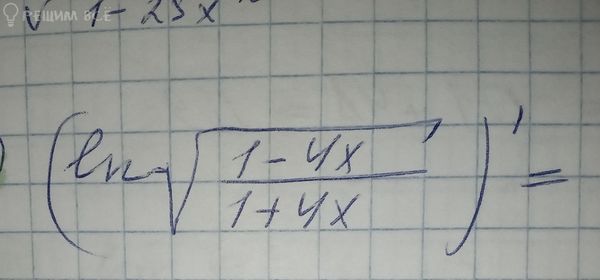
121
Решение
★
f(x) = ln(g(x))
g(x) = sqrt(h(x))
[m]h(x) = \frac{1-4x}{1+4x} =-\frac{4x-1}{4x+1} = -\frac{4x+1-2}{4x+1} = -1 + \frac{2}{4x+1}[/m]
Берем производную:
[m] f'(x) =\frac{1}{g(x)} \cdot g'(x) = \frac{g'(x)}{g(x)}[/m]
[m] g'(x) = \frac{h'(x)}{2\sqrt{h(x)}}[/m]
[m] h'(x) = - \frac{2*4}{(4x+1)^2} = - \frac{8}{(4x+1)^2}[/m]
Дальше подставляет, извините, у меня времени нет, закончите сами.