Задача 679 Решите уравнение 6sin^2x+7cosx-7=0 и...
Условие
математика 10-11 класс
166694
Решение
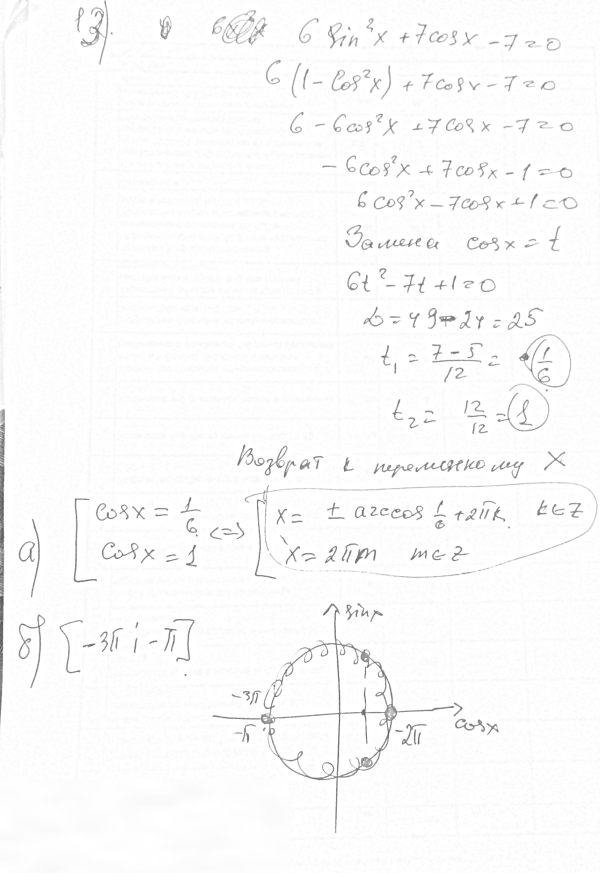
Ответ: В решение
Все решения
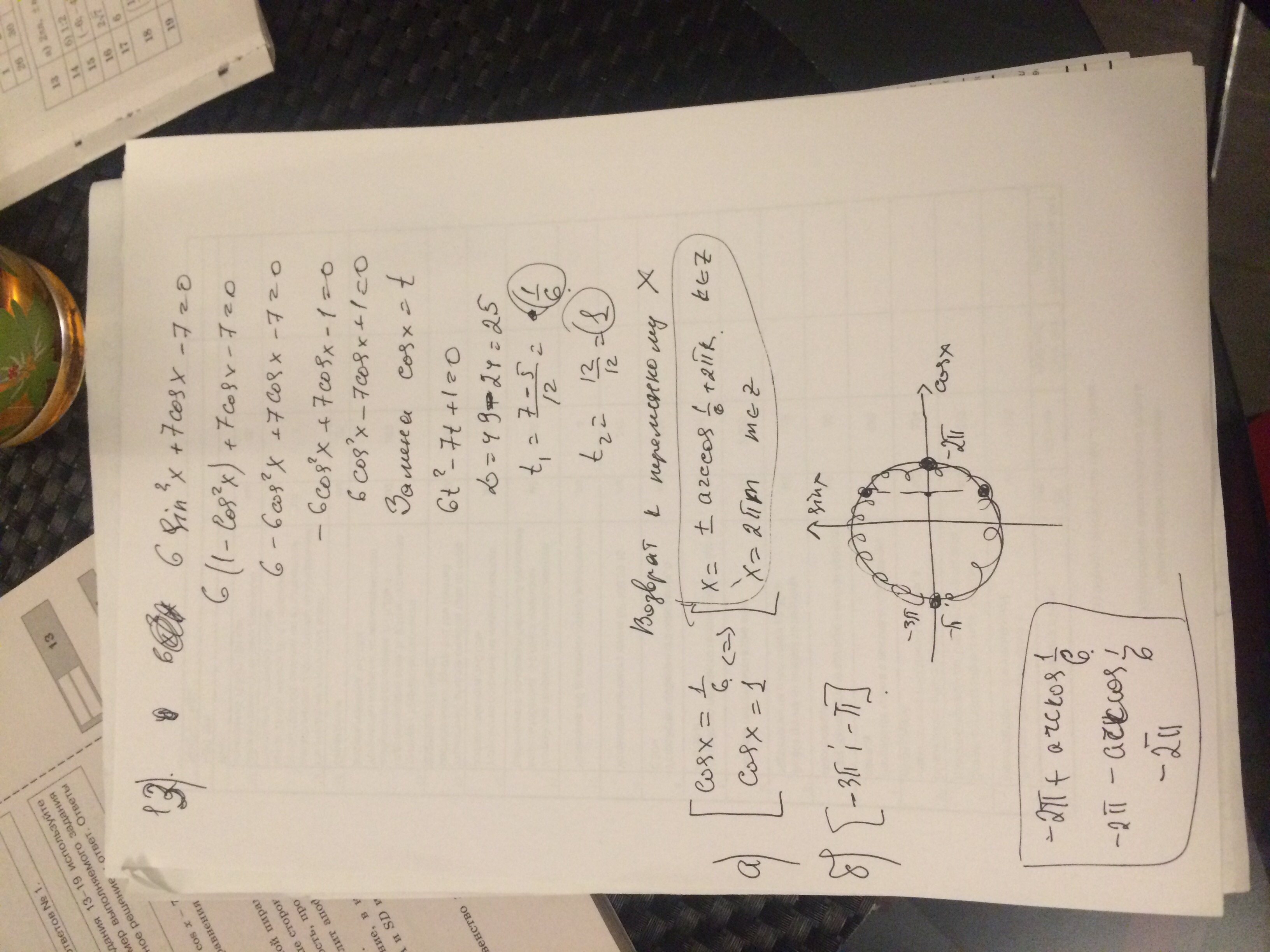

Ответ: В решение
