Задача 67884 задания по алгебре ...
Условие

Решение
1)[m] ∫ _{0}^{2}x^3dx=(\frac{x^4}{4})|_{0}^{2}=\frac{2^4}{4}-\frac{0^4}{4}=4[/m]
2)[m] ∫ _{-1}^{2}e^{x}dx=(e^{x})|_{-1}^{2}=e^{2}-e^{-1}=e^2-\frac{1}{e}=\frac{e^3-1}{e}[/m]
3)[m] ∫ _{0}^{\frac{π}{6}}cosxdx=(sinx)|_ {0}^{\frac{π}{6}}=sin\frac{π}{6}-sin0=\frac{1}{2}[/m]
[b]2.[/b]
[m] S=∫ _{0}^{1}((x+2)-(x^2+2))dx=∫ _{0}^{1}(x+2-x^2-2)dx=∫ _{0}^{1}(x-x^2)dx=(\frac{x^2}{2}-\frac{x^3}{3})|_{0}^{1}=(\frac{1^2}{2}-\frac{1^3}{3})-(\frac{0^2}{2}-\frac{0^3}{3})=\frac{1}{2}-\frac{1}{3}-0=\frac{1}{6}[/m]
[b]3.[/b]
1)[m]∫ _{-1}^{1}(x-1)^5dx=∫ _{-1}^{1}(x-1)^5d(x-1)=(\frac{(x-1)^5}{5})|_{-1}^{1}=\frac{(1-1)^5}{5}-\frac{(-1-1)^5}{5}=\frac{32}{5}[/m]
2)[m] ∫ _{π}^{3π}sin\frac{x}{3}dx=∫ _{π}^{3π}sin\frac{x}{3}3d(\frac{x}{3})=3\cdot (-cos\frac{x}{3})| _{π}^{3π}=-3\cdot (cos\frac{3π}{3}-cos\frac{π}{3})=-3\cdot (cosπ)+3\cdot cos\frac{π}{3}=3\cdot (-1)+3\cdot \frac{1}{2}=4,5[/m]
4.
Уравнение касательной к кривой [m] y=f(x)[/m] в точке с абсциссой [m]x_{o}[/m]
[m]y-f(x_{o})=f`(x_{o})\cdot (x-x_{o})[/m]
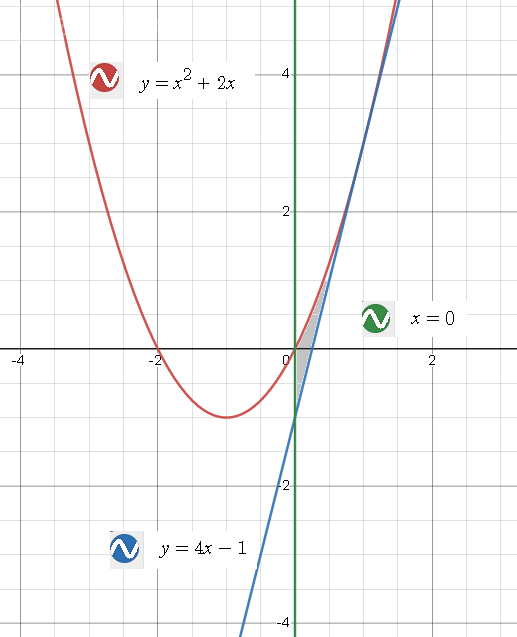
[m]f(x)=x^2+2x[/m]
[m]f`(x)=(x^2+2x)`=2x+2[/m]
[m]x_{o}=1[/m]
[m]f(x_{o})=f(1)=1^2+2\cdot 1=1+2=3[/m]
[m]f`(x_{o})=f`(1)=2\cdot 1+2=4[/m]
Уравнение касательной в точке с абсциссой [m]x_{o}=1[/m]
[m]y-3=4\cdot (x-1)[/m] ⇒[red] [m]y=4x-1[/m] [/red]
[m]S=∫ _{0}^{1}((x^2+2x)-(4x-1))dx=∫ _{0}^{1}(x^2+2x-4x+1)dx=[/m]
[m]=∫ _{0}^{1}(x^2-2x+1)dx=∫ _{0}^{1}(x-1)^2dx=∫ _{0}^{1}(x-1)^2d(x-1)=\frac{(x-1)^3}{3}|_{0}^{1}(x-1)^2=\frac{(1-1)^3}{3}-\frac{(0-1)^3}{3}=\frac{1}{3}[/m]