Задача 67839 задача по геометрии...
Условие

105
Решение
★
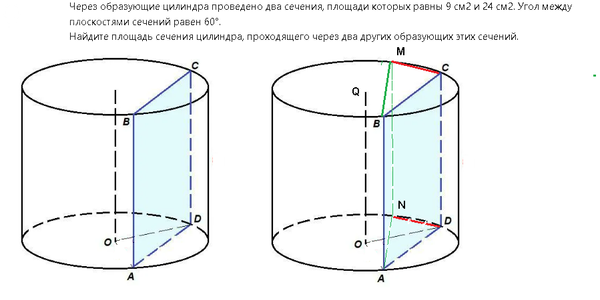
S_(ABMN)=9
∠ NAD= ∠ MBC=60 °
Найти S_(MNDC)=
S_(АВСD)=AD*CD ⇒ 24=[b]AD*CD[/b] ⇒ CD=24/AD
S_(ABMN)=AN*MN ⇒ 9=AN*MN ⇒ MN=9/AN
MN=CD ⇒ 24/AD=9/AN ⇒ 24*AN=9*AD
8*AN=3*AD ⇒ AN=(3/8)AD
S_(MNDC)=ND*CD
По теореме косинусов
ND^2=AD^2+AN^2-2AD*AN*cos ∠ NAD
ND^2=AD^2+((3/8)AD)^2-2AD*(3/8)AD*cos ∠ 60 °
ND^2=AD^2+(9/64)AD^2-2AD*(3/8)AD*(1/2)
ND^2=AD^2+(9/64)AD^2-(3/8)AD^2
ND^2=(1+(9/64)-(3/8))AD^2
ND^2=(49/64)AD^2
ND=(7/8)AD
S_(MNDC)=ND*CD=(7/8)*[b]AD*CD[/b]=(7/8)*24=21 см^2