Задача 67703 ...
Условие
cos2x+a≤2√(x^2+16)-(x^2+16)/(a+cos2x)
имеет единственное решение.
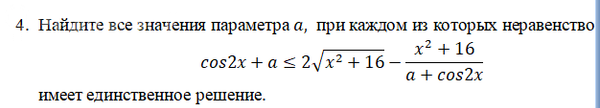
Решение
Область определения:
cos 2x + a ≠ 0
cos 2x ≠ - a
Умножаем всё неравенство на (cos 2x + a):
(cos 2x + a)^2 ≤ 2sqrt(x^2+16)(cos 2x + a) - (x^2+16)
(cos 2x + a)^2 - 2sqrt(x^2+16)(cos 2x + a) + (x^2+16) ≤ 0
Это формула квадрата разности:
(cos 2x + a - sqrt(x^2+16))^2 ≤ 0
Квадрат любого выражения есть число неотрицательное.
Поэтому неравенство превращается в уравнение:
cos 2x + a - sqrt(x^2+16) = 0
cos 2x + a = sqrt(x^2+16)
Заметим, что cos 2x - функция чётная.
sqrt(x^2+16) - тоже функция чётная.
Поэтому, если есть решение х, то будет и решение -х.
Если решение единственное, то очевидно, должно быть x = 0.
cos 0 + a = sqrt(16)
1 + a = 4
a = 3
Ответ: при а = 3 единственное решение x = 0.