Задача 67695 можете решить задания по алгебре ...
Условие
Решение
По формуле Ньютона Лейбница:
1)
[m] ∫ _{1}^{2}x^4dx=(\frac{x^5}{5})| _{1}^{2}=\frac{2^5}{5}-\frac{1^5}{5}=\frac{31}{5}[/m]
2)
[m] ∫_{\frac{π}{6}} ^{2π}cosxdx= (sinx)|_{\frac{π}{6}} ^{2π}=sin 2π -sin \frac{π}{6}=0-\frac{1}{2}=-0,5[/m]
2.
[m] S=∫ _{2}^{5}(f(x)-g(x))dx[/m]
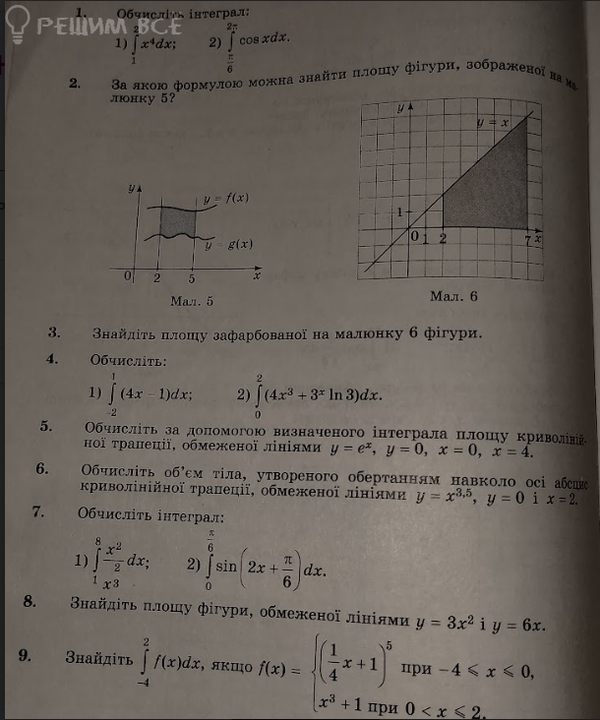
3.
[m]S= ∫ _{2}^{7}(f(x)-g(x))dx[/m]
[m]f(x)=x[/m]
[m]g(x)=0[/m]
[m] S=∫ _{2}^{7}x dx=(\frac{x^2}{2})|_{2}^{7}=\frac{7^2}{2}-(\frac{2^2}{2})=\frac{45}{2}=22,5[/m]
4.
1)
[m] ∫ _{-2}^{1}(4x-1)dx=∫ _{-2}^{1}4xdx-∫ _{-2}^{1}dx=4∫ _{-2}^{1}xdx-∫ _{-2}^{1}dx=(4\cdot \frac{x^2}{2})| _{-2}^{1}-(x)| _{-2}^{1}=2\cdot 1^2-2\cdot (-2)^2-(1-(-2))=-9[/m]
2)
[m] ∫ _{0}^{2}(4x^3+3^{x}ln3)dx=∫ _{0}^{2}4x^3dx+∫ _{0}^{2}3^{x}ln3dx=4∫ _{0}^{2}x^3dx+ln3∫ _{0}^{2}3^{x}dx=(4\cdot \frac{x^4}{4})|_{0}^{2}+ln3\cdot( \frac{3^{x}}{ln3})|_{0}^{2}=2^4+3^2-3^{0}=16+9-1=24[/m]
5.
[m] ∫ _{0}^{4}e^{x}dx=(e^{x})| _{0}^{4}=e^4-e^{0}=e^{4}-1[/m]
6.
[m]V_{Ox}=π ∫ _{0}^{2}(x^{3,5})^2dx=π ∫ _{0}^{2}x^{2\cdot 3,5}dx=π ∫ _{0}^{2}x^{7}dx=(\frac{x^8}{8})| _{0}^{2}=\frac{2^8}{8}-0=32[/m]