Задача 67666 Помощь в алгебре Даю 30 баллов !...
Условие
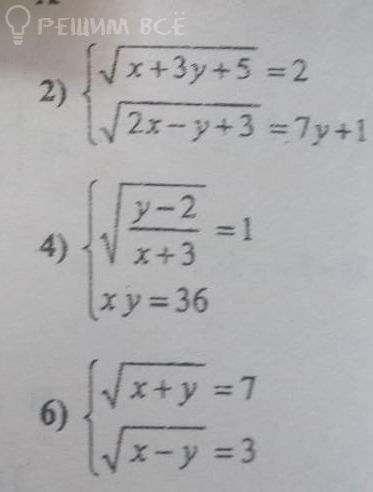
Решение
{ sqrt(x + 3y + 5) = 2
{ sqrt(2x - y + 3) = 7y + 1
Область определения:
{ x + 3y + 5 ≥ 0
{ 2x - y + 3 ≥ 0
{ 7y + 1 ≥ 0
Я не буду решать эту систему неравенств, проще решить систему уравнений, а потом найденные числа подставить в эту систему.
Возводим оба уравнения в квадрат:
{ x + 3y + 5 = 4
{ 2x - y + 3 = (7y + 1)^2
Раскрываем скобки:
{ x + 3y + 1 = 0
{ 2x - y + 3 = 49y^2 + 14y + 1
Приводим подобные:
{ x + 3y + 1 = 0
{ 2x = 49y^2 + 15y - 2
Решаем подстановкой:
{ x = 24,5y^2 + 7,5y - 1
{ 24,5y^2 + 7,5y - 1 + 3y + 1 = 0
Получаем квадратное уравнение:
24,5y^2 + 10,5y = 0
y1 = 0; x1 = -1 - по области определения подходит.
y2 = -10,5/24,5 = -21/49 = -3/7
7y + 1 = -3 + 1 = -2 < 0 - не подходит по области определения.
x2 можно уже не вычислять.
Ответ: (-1; 0)
4) Система уравнений:
{ sqrt((y - 2)/(x + 3)) = 1
{ xy = 36
Область определения:
{ (y - 2)/(x + 3) ≥ 0
{ x ≠ -3
Решаем систему уравнений. Возводим в квадрат 1 уравнение:
{ (y - 2)/(x + 3) = 1
{ xy = 36
Умножаем 1 уравнение на (x + 3):
{ y - 2 = x + 3
{ xy = 36
Решаем подстановкой:
{ y = x + 5
{ x(x + 5) = 36
x^2 + 5x - 36 = 0
(x + 9)(x - 4) = 0
x1 = -9; y1 = x + 5 = -4 - подходит по области определения.
x2 = 4; y2 = 9 - подходит по области определения.
Ответ: (-9; -4); (4; 9)
6) Система уравнений:
{ sqrt(x + y) = 7
{ sqrt(x - y) = 3
Область определения:
{ x + y ≥ 0
{ x - y ≥ 0
Решаем систему уравнений. Возводим в квадрат оба уравнения:
{ x + y = 49
{ x - y = 9
Складываем уравнения:
2x = 58
x = 29
y = 49 - x = 49 - 29 = 20
Подходит по области определения.
Ответ: (29; 20)