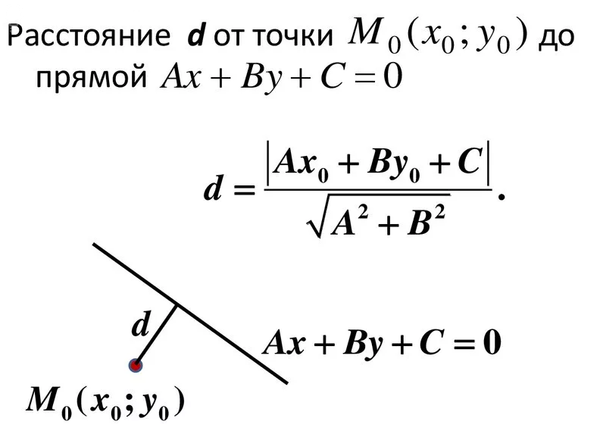Задача 67641 В треугольнике АВС, заданном...

639e2b43d3c6e55759ed9abf

17.12.2022 23:51:27

В треугольнике АВС, заданном координатами вершин: А (4, 1),
В (1, -2), С (-5, 7) проведена высота АН, найти ее уравнение и длину.

5f3ea7e3faf909182968ddd9

18.12.2022 09:53:40

★

Составляем уравнение стороны BC

[m]\frac{x-1}{-5-1}=\frac{y-(-2)}{7-(-2)}[/m]

[m]\frac{x-1}{-6}=\frac{y+2}{9}[/m]

Применяем основное свойство пропорции

⇒ [m]9(x-1)=-6(y+2)[/m]

Сокращаем на 3:

[m]3(x-1)=-2(y+2)[/m]

Раскрываем скобки, приводим подобные

[m]3x+2y+1=0[/m] - общее уравнение прямой ВС

[m]y=-(3/2)x-(1/2)[/m]- уравнение прямой ВС с угловым коэффициентом

угловой коэффициент прямой ВС

k_(BC)=-(3/2)

Произведение угловых коэффициентов перпендикулярных прямых равно (-1)

k_(BC)*k_(АН)=-1

Значит, угловой коэффициент любой прямой перпендикулярной ВC равен

([b][/b]2/3)

Общий вид таких прямых

y=[b](2/3)[/b]x+b

Подставляем координаты точки А и находим b

1=(2/3)*4+b

b=-5/3

уравнение высоты АH:

[b]y=(2/3)x-(5/3)[/b]

или

[b]2x-3y-5=0[/b]


Найдем координаты точки Н - точки пересечения ВС и высоты АН

Решаем систему уравнений:

{y=-(3/2)x-(1/2)
{y=(2/3)x-(5/3)

Приравниваем правые части

-(3/2)x-(1/2)=(2/3)x-(5/3)

-(3/2)x-(2/3)x=-(5/3)+(1/2)

-(13/6)x=-(7/6)

x=7/13

y=-17/13

H(7/13; -17/13)

[m]AH=\sqrt{(\frac{7}{13}-4)^2+(-\frac{17}{13}-1)^2}=\frac{\sqrt{(-45)^2+(-30)^2}}{13}=\frac{15\sqrt{13}}{13}[/m]


С другой стороны, длина высоты - это расстояние от точки А до прямой ВС

Применяем формулу ( см. скрин)

уравнение BC:[m]3x+2y+1=0[/m]

[m]d=\frac{|3\cdot 4+2\cdot 1+1|}{\sqrt{3^2+2^2}}=\frac{15}{\sqrt{13}}=\frac{15\sqrt{13}}{13}[/m]