Задача 676 Найдите наибольшее значение функции...
Условие
математика 10-11 класс
33009
Решение
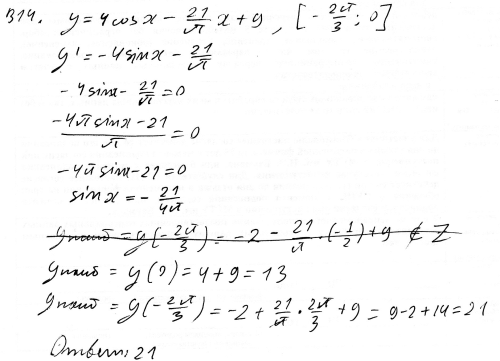
Ответ: 21
Все решения
y=4cosx-21x/p+9 yfqnb Yнаиб на отрезке [-2p/3;0]
Найдем стационарные точки: y*=-4sinx-21/p Замечаем,что y* < 0 так как |sinx| < =1.Следовательно функция убывает и наибольшее свое значение принимает на левом конце при x=-2p/3. Вычислим его: Y(-2p/3)=4*cos(-2p/3)+21/p*2p/3+9=4*(-1/2)+14+9=21
Ответ: 21.
