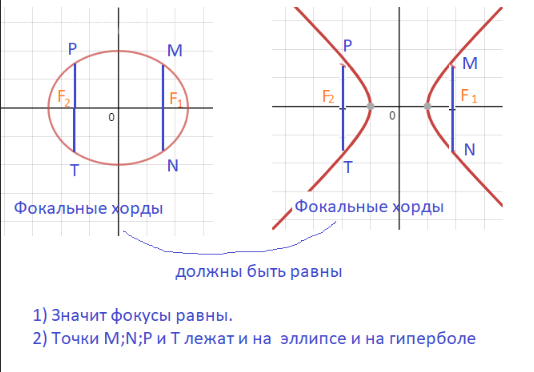
Задача 67282 [b]Составить каноническое уравнение...
Условие
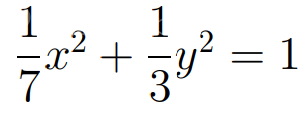
Решение
(x^2/a^2)+(y^2/b^2)=1
a^2=b^2+c^2 ⇒ c^2=a^2-b^2
Данное уравнение можно записать в таком же виде:
(x^2/7)+(y^2/3)=1
⇒
a^2=7 ⇒ a=sqrt(7)
b^2=3 ⇒ b=sqrt(3)
c^2=a^2-b^2=7-3=4
c=2
F_(1)(-2;0); F_(2)(2;0) - фокусы эллипса.
Точки P и Т лежат на прямой, проходящей через фокус F_(1(-2;0)
Значит абсцисса этих точек х=-2
Найдем ординаты точек P и Т
подставим x=-2 в уравнение
(x^2/7)+(y^2/3)=1
y^2=3*(1-(4/7)
y^2=9/7
y= ± 3/sqrt(7)
Фокальная хорда РТ=(3/sqrt(7))-(-3/sqrt(7))=6/sqrt(7)
Каноническое уравнение гиперболы:
(x^2/a^2)-(y^2/b^2)=1
с^2=a^2+b^2
a и b неизвестны, а
c=2 как и у эллипса
F_(1)(-2;0); F_(2)(2;0) - фокусы гиперболы
Найдем ординаты.
подставим x=-2 в уравнение
(x^2/a^2)-(y^2/b^2)=1
(y^2/b^2)=(4/a^2)-1
Ординаты такие же
b^2((4/a^2)-1)=3*(1-(4/7)
и
a^2+b^2=2^2 ⇒ b^2=4-a^2 и подставляем в первое
a^2=3*(3/7) ⇒
a^2=9/7
b^2=4-(9/7)=19/7
x^2/(9/7)-(y^2/19/7))=1 - уравнение искомой гиперболы