Задача 67071 ...
Условие
нет в списке 10-11 класс
143
Решение
★
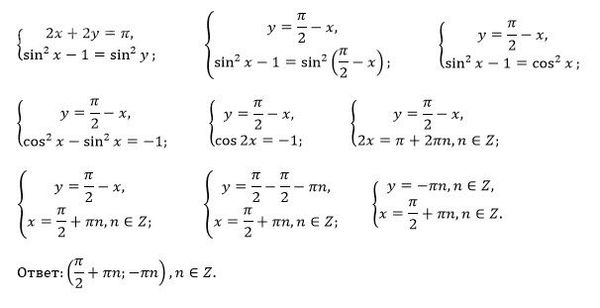
Все решения
{ sin^2 x - 1 = sin^2 y
Решаем подстановкой:
{ y = π/2 - x
{ sin^2 x - 1 = sin^2 (π/2 - x)
По формулам приведения:
sin^2 x - 1 = -cos^2 x
sin (π/2 - x) = cos x
Получаем:
{ y = π/2 - x
{ -cos^2 x = cos^2 x
Из 2 уравнения сразу:
cos x = 0
x = π/2 + π*n, n ∈ Z
y = π/2 - x = π/2 - (π/2 + π*n) = -π*n, n ∈ Z
Ответ: x = π/2 + π*n; y = -π*n, n ∈ Z