Задача 66997 Найти интегралы. Результаты проверить...
Условие
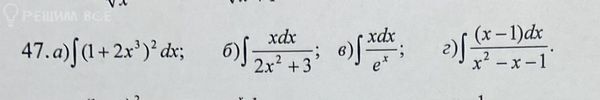
Решение
Раскрываем скобки:
(1+2x^3)^2=1+2*2x^3+(2x^3)^2=1+4x^3+4x^6
∫ (1+2x^3)^2dx= ∫ (1+4x^3+4x^6)dx= ∫1dx+4 ∫ x^3dx+4 ∫ x^6dx=x+4*(x^4/4)+4*(x^7/7)+C=[b]x+x^4+(4/7)x^7+C[/b]
Проверка
([b]x+x^4+4*(x^7/7)+C[/b])`=(x)`+(x^4)`+(4/7)(x^7)`+C`=1+4x^3+4x^6+0=(1+2x^3)^2
б)
∫ xdx/(2x^2+3)
Применяем формулу
∫ du/u= ln|u|+C
[red]Замена[/red]
[b]u=2x^2+3[/b] ⇒ du=(2x^2+3)`dx ⇒ du=4x dx
xdx=du/4
∫ xdx/(2x^2+3)= ∫ (du/4)/u=(1/4) ∫ du/u=(1/4)ln|u|+C=(1/4)ln|2x^2+3|+C=[b](1/4)ln(2x^2+3)+C[/b]
Проверка
([b](1/4)ln(2x^2+3)+C[/b])`=(1/4)*(ln(2x^2+3))`+C`=(1/4)*(1/(2x^2+3))*(2x^2+3)`+0=(1/4)*(1/(2x^2+2))*(4x)=x/(2x^2+3)
в) задавайте отдельным вопросом
г) задавайте отдельным вопросом