Задача 66747 Обчислити нескінченну суму...
Условие
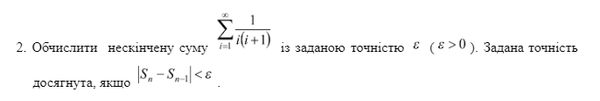
Решение
[m]\frac{1}{i(i+1)}=\frac{1}{i}-\frac{1}{i+1}[/m]
[m]S_{n}= ∑_{i=1}^{n}(\frac{1}{i}-\frac{1}{i+1})=(\frac{1}{1}-\frac{1}{1+1})+(\frac{1}{2}-\frac{1}{2+1})+... +(\frac{1}{n}-\frac{1}{n+1}) [/m] ⇒
[m]S_{n}=(\frac{1}{1}-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}... -\frac{1}{n+1} [/m]
[m]S_{n}=1-\frac{1}{n+1} [/m]
По условию:
[m]S_{n}-S_{n-1}=\frac{1}{n(n+1)}=[/m] ⇒
[m]|S_{n}-S_{n-1}|=|\frac{1}{n(n+1)}|=\frac{1}{n(n+1)} < ε [/m] ⇒ [m] n(n+1) > \frac{1}{ ε }[/m] ⇒ зная конкретное ε
найдем n, т.е сколько слагаемых в сумме
[m]S_{n}=1-\frac{1}{n+1} [/m]
если n=10
[m]S_{10}=1-\frac{1}{10+1}=\frac{10}{11} [/m] это 0, 909090....
точность маленькая. только первая цифра после запятой
если n=1000
[m]S_{1000}=1-\frac{1}{1000+1}=\frac{1000}{1001} [/m] это 0, 99990001
точность лучше