Задача 66720 Даны две противоположные вершины...
Условие
Решение
Уравнение АС:
[m]\frac{x-(-5)}{3-(-5)}=\frac{y-2}{-4-2}[/m] ⇒ [m]\frac{x+5}{8}=\frac{y-2}{-6}[/m]
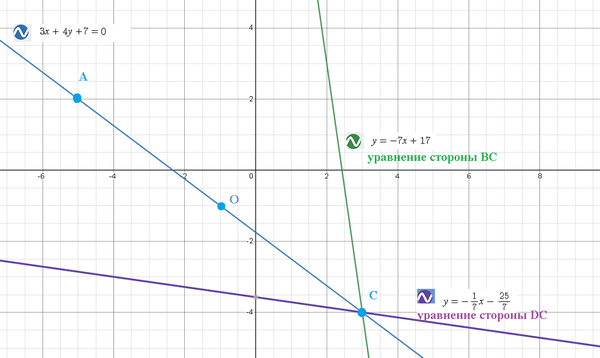
3x+4y+7=0
[m]y=-\frac{3}{4}x-\frac{7}{4}[/m]
[m]k_{AC}=-\frac{3}{4}[/m]
Найдем
[m]k_{BC}[/m]
Так как угол между АС и ВС равен 45 °
применяем формулу:
По формуле:
[m]tgφ=|\frac{k_{2}−k_{1}}{1+k_{1}⋅k_{2}}|[/m]
[m]tg45°=|\frac{k_{BC}−(-\frac{3}{4})}{1+(-\frac{3}{4})⋅k_{BC}}|[/m] ⇒
[m]1=|\frac{k_{BC}−(-\frac{3}{4})}{1+(-\frac{3}{4})⋅k_{BC}}|[/m] ⇒[m]\frac{k_{BC}−(-\frac{3}{4})}{1+(-\frac{3}{4})⋅k_{BC}}= ±1 [/m]
[m]1-\frac{3}{4}k_{BC}=k_{BC}+\frac{3}{4}[/m] или [m]1-\frac{3}{4}k_{BC}=-k_{BC}-\frac{3}{4}[/m]
[m]k_{BC}=-\frac{1}{7}[/m] или [m]k_{BC}=7[/m]
Уравнение прямой принимает вид
[m]y=-\frac{1}{7}x+m[/m] или [m]y=-7x+n[/m]
Чтобы найти m и n подставим координаты точки C (3;-4), через которую проходит прямая.
[m]-4=-\frac{1}{7}\cdot 3+m[/m] ⇒ [m]m=-\frac{25}{7}[/m] ⇒ [m]y=-\frac{1}{7}x-\frac{25}{7}[/m]
или
[m]-4=-7\cdot 3+n[/m] ⇒ [m] n=17[/m] ⇒ [m]y=-7x+17[/m]
O(-1; -1) - середина АС
AD || BC
Угловые коэффициента параллельных прямых равны:
AD: [m]y=-7x+b[/m]
Чтобы найти m]b[/m] подставляем координаты точки А
AB || CD
AB :[m]y=-\frac{1}{7}x+p[/m]
Чтобы найти [m]p[/m] подставляем координаты точки А