Задача 664 a) Решите уравнение...
Условие
б) Укажите корни, принадлежащие отрезку [5Pi/2;7PI/2]
математика 10-11 класс
50469
Решение
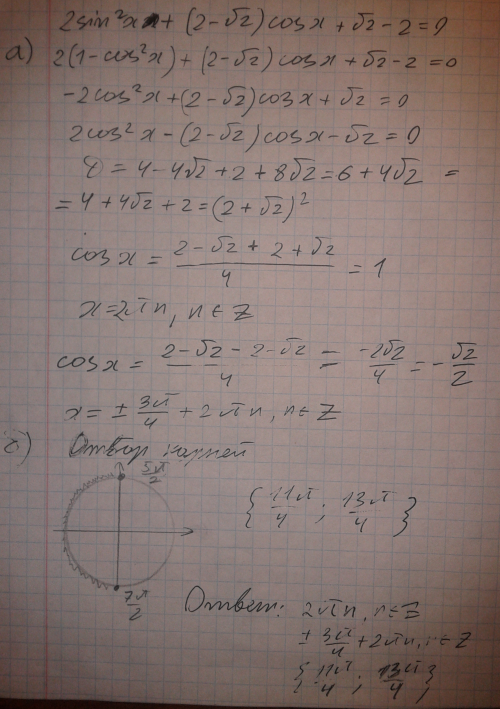
Ответ: В решение
б) Укажите корни, принадлежащие отрезку [5Pi/2;7PI/2]
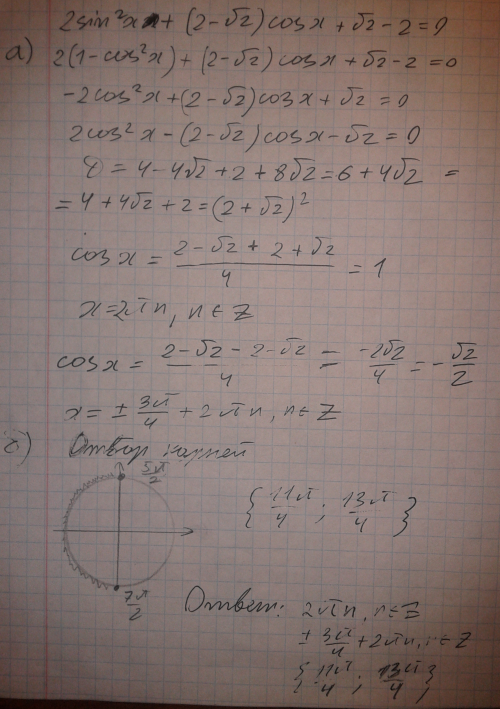
Ответ: В решение