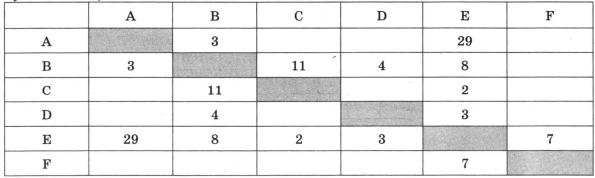
Между населёнными пунктами А, В, С, D, Е, F построены дороги, протяжённость которых приведена в таблице. (Отсутствие числа в таблице означает, что прямой дороги между пунктами нет.)
Определите длину кратчайшего пути между пунктами А и F (при условии, что передвигаться можно только по построенным дорогам).
информатика 10-11 класс
5236
В пункт F построена дорога только из пункта Е, поэтому надо искать кратчайший путь из пункта А в пункт Е. Прямая дорога из А в Е имеет протяженность 29 км, а через пункты В и D совокупная протяженность пути из А в Е составит 3+4+3=10 км. Прибавим к этому расстояние от Е до F (7 км) и получим общую протяженность маршрута 10+7=17 км.
Ответ: 17
