Задача 65700 В одной и той же системе координат...
Условие
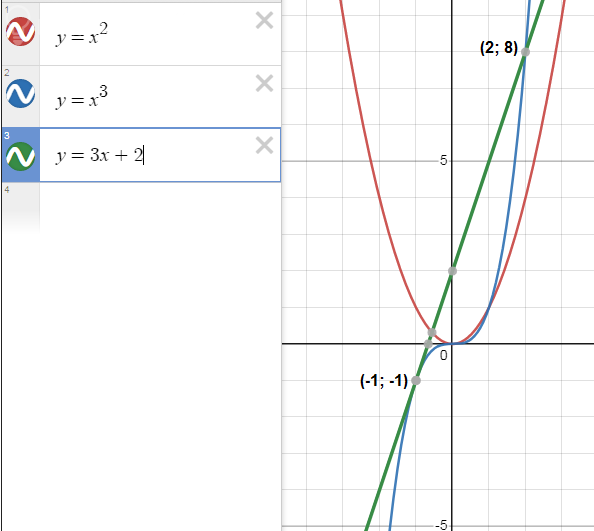
функций ???? = ????2, ???? = ????3 и ???? = 3???? + 2. Решите графически
уравнение ????3 = 3???? + 2.
математика 6-7 класс
885
Решение
★
y = x^2; y = x^3; y = 3x + 2
Решением уравнения
x^3 = 3x + 2
Являются две точки: (-1; -1); (2; 8)
То, что прямая y = 3x + 2 - касательная к y = x^3, означает, что этот корень (-1) - кратный, то есть двойной.
Если решать аналитически, то получится:
x^3 - 3x - 2 = 0
x^3 + x^2 - x^2 - x - 2x - 2 = 0
x^2(x + 1) - x(x + 1) - 2(x + 1) = 0
(x + 1)(x^2 - x - 2) = 0
(x + 1)(x^2 + x - 2x - 2) = 0
(x + 1)(x(x + 1) - 2(x + 1)) = 0
(x + 1)(x + 1)(x - 2) = 0
x1 = x2 = -1; x3 = 2