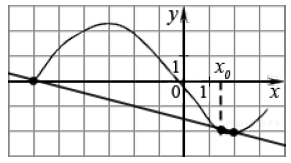
Задача 656 На рисунке изображён график функции...
Условие
математика 10-11 класс
19615
Решение
y'(x0)=tg(180-ACB)=-tg(ACB)=-AB/BC=-0.25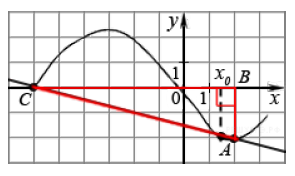
Ответ: -0.25

y'(x0)=tg(180-ACB)=-tg(ACB)=-AB/BC=-0.25
Ответ: -0.25