Задача 65388 ...
Условие
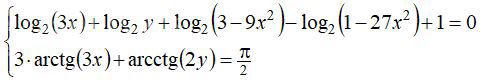
Решение
[m]\left\{\begin {matrix}3x>0\\y>0\\3-9x^2>0\\1-27x^2>0\end {matrix}\right.[/m] ⇒ x ∈ (0;sqrt(3)/9)
Первое уравнение:
так как [m]1=log_{2}2[/m]
[m]log_{2}(3x)+log_{2} y+log_{2} (3-9x^2)+log_{2}2=log_{2}(1-27x^2)[/m]
Заменим сумму логарифмов логарифмом произведения
[m]log_{2}(3x)\cdot y\cdot (3-9x^2)\cdot 2=log_{2}(1-27x^2)[/m]
[m](3x)\cdot y\cdot (3-9x^2)\cdot 2=1-27x^2[/m] ⇒ [m]y=\frac{1-27x^2}{6x(3-9x^2)}[/m]
Второе уравнение:
[m]3arctg(3x)+arcctg2y=\frac{π}{2}[/m]
Замена:
[m]arctg 3x= α [/m] ⇒ [m]tg α =3x[/m] ⇒[m]x=\frac{tgα}{3}[/m]
[m]arcctg2y= β [/m] ⇒ [m]ctg β = 2y[/m]
Второе уравнение принимает вид
[m]3 α + β =\frac{π}{2}[/m] ⇒ [m] β =\frac{π}{2}-3 α [/m]
[red][m]ctg β = 2y[/m] [/red]
[red][m]ctg (\frac{π}{2}-3 α) = 2y[/m] [/red]
[red][m]ctg (\frac{π}{2}-3 α) = 2\frac{1-27x^2}{6x(3-9x^2)}[/m] [/red]
Подставим:
[m]x=\frac{tgα}{3}[/m]
Применим формулы приведения, получим
[red][m]tg 3α =\frac{1-3tg^2 α }{tg α (3-tg^2 α )}[/m] [/red]
Так как
[m]tg3 α =tg( α +2 α )[/m]
Применяем формулу [r] [m]tg(x+y)=\frac{tgx+tgy}{1-tgx\cdot tgy}[/m][/r]
[m]tg3 α =\frac{tg α+tg2 α }{1-tg α \cdot tg2 α }[/m]
По той же формуле:
[m]tg2 α =\frac{2tg α }{1-tg^2 α }[/m]
⇒
[m]tg3 α =\frac{tg α+\frac{2tg α }{1-tg^2 α } }{1-tg α \cdot \frac{2tg α }{1-tg^2 α } }[/m]
[m]tg3 α =\frac{tg α-tg^3 α +2tg α }{1-tg^2 α -2tg^2 α}[/m]
[m]tg3 α =\frac{3tg α -tg^3 α }{1-3tg^2 α }[/m]
уравнение можно записать в виде
[red][m]\frac{1-3tg^2 α } {3tg α -tg^3 α } =\frac{1-3tg^2 α }{tg α (3-tg^2 α )}[/m] [/red]
Получили верное равенство, т. е тождество, которое верно при любых х , принадлежащих ОДЗ
Значит ответ
x ∈ (0;sqrt(3)/9)
y ∈ (0;+ ∞ )
[m]y=\frac{1-27x^2}{6x(3-9x^2)}[/m]