Задача 65327 готовлюсь ко вступительным экзаменам,...
Условие
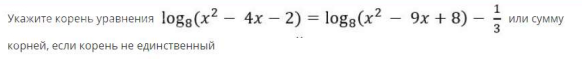
Решение
⇒
[m]\frac{1}{3}=\frac{1}{3}\cdot 1=\frac{1}{3}\cdot log_{8}8= log_{8}8^{\frac{1}{3}}= log_{8}2[/m]
⇒
Уравнение принимает вид:
[m]log_{8}(x^2-4x-2)=log_{8}(x^2-9x+8)-log_{8}2[/m]
[m]log_{8}(x^2-4x-2)+log_{8}2=log_{8}(x^2-9x+8)[/m]
Cумму логарифмов заменим логарифмом произведения:
[m]log_{8}(x^2-4x-2)\cdot 2=log_{8}(x^2-9x+8)[/m]
Логарифмическая функция монотонно возрастает.
Значит каждое свое значение принимает один раз, т.е в одной точке.
Если значения функции равны, то точка одна и та же,
другими словами аргументы равны
[m](x^2-4x-2)\cdot 2=x^2-9x+8[/m]
[m]2x^2-8x-4=x^2-9x+8[/m]
[m]2x^2-8x-4-x^2+9x-8=0[/m]
[m]x^2+x-12=0[/m]
D=1+48=49
x_(1)=-4; x_(2)=3
ПРОВЕРКА
При
х=-4
[m]log_{8}((-4)^2-4\cdot (-4)-2)=log_{8}((-4)^2-9\cdot (-4)+8)-\frac{1}{3}[/m]
[m]log_{8}30=log_{8}60-log_{8}2[/m]
[m]log_{8}30\cdot 2=log_{8}60[/m]- верно.
При
х=3
[m]log_{8}((3)^2-4\cdot (3)-2)[/m] не существует
х=3 - посторонний корень
О т в е т. x=-4
Вместо проверки можно решать уравнение c нахождением ОДЗ уравнения
ОДЗ:
[m]\left\{\begin {matrix}x^2-4x-2>0\\x^2-9x+8>0\end {matrix}\right.[/m] ⇒
[m]\left\{\begin {matrix}D=24; тогда... решение... неравенства... x<2-\sqrt{6}... или... x> 2+\sqrt{6}\\D=49; тогда ... решение... неравенства... x < 1... или... x> 8\end {matrix}\right.[/m]
ОДЗ:[m] x ∈ (- ∞ ; 2-\sqrt{6})\cup (8;+ ∞ )[/m]
-4 ∈ ОДЗ
3 ∉ ОДЗ