Задача 65163 решить уравнения...
Условие
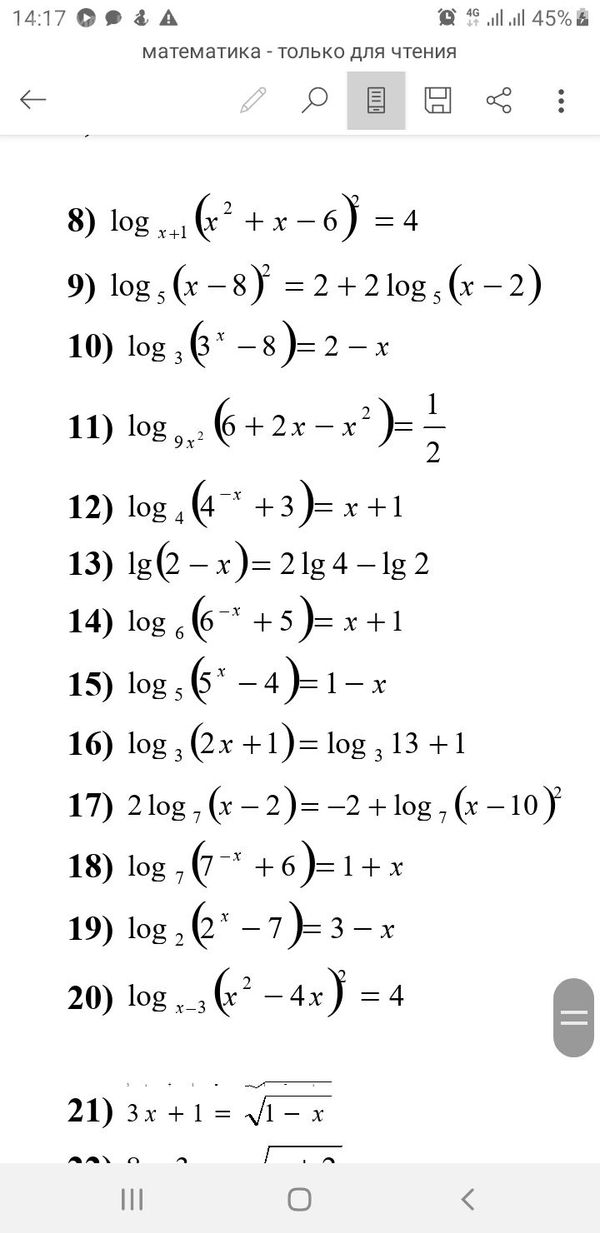
Решение
ОДЗ:
{ x+1 > 0; x+1 ≠ 1
{ x^2 + x - 6 > 0
Решаем:
{ x ∈ (-1; 0) U (0; +oo)
{ (x+3)(x-2) > 0
Получаем:
x ∈ (2; +oo)
Решаем уравнение.
Степень выносится и умножается на логарифм
2log_(x+1) (x^2 + x - 6) = 4
log_(x+1) (x^2 + x - 6) = 2
По определению логарифма:
(x+1)^2 = x^2 + x - 6
x^2 + 2x + 1 = x^2 + x - 6
2x + 1 = x - 6
x = -7 < 2
Но по ОДЗ: x > 2, поэтому
Ответ: Корней нет.
Дальше я не буду так подробно расписывать, там всё тоже самое.
9) log_5 (x-8)^2 = 2 + 2log_5 (x-2)
ОДЗ:
{ x ≠ 8
{ x > 2
x ∈ (2; 8) U (8; +oo)
Решаем уравнение:
2log_5 (x-8) = 2 + 2log_5 (x-2)
log_5 (x-8) = 1 + log_5 (x-2) = log_5 (5) + log_5 (x-2)
log_5 (x-8) = log_5 (5x-10)
x - 8 = 5x - 10
10 - 8 = 5x - x
4x = 2
x = 1/2 < 2 - не подходит по ОДЗ.
Ответ: Корней нет.
10) log_3 (3^x - 8) = 2 - x
ОДЗ:
3^x - 8 > 0
3^x > 8
x > log_3 8
x ∈ (log_3 8; +oo)
Решаем уравнение:
3^(2 - x) = 3^x - 8
3^2 : 3^x = 3^x - 8
Замена y = 3^x > 0 при любом x.
9/y = y - 8
9 = y^2 - 8y
y^2 - 8y - 9 = 0
(y +1)(y - 9) = 0
y = -1 < 0 - не подходит
y = 9 - подходит.
3^x = 9
x = 2 > log_3 8 - подходит.
Ответ: x = 2
11) log_(9x^2) (6 + 2x - x^2) = 1/2
ОДЗ:
{ 9x^2 > 0; 9x^2 ≠ 1
{ -x^2 + 2x + 6 > 0
Решаем:
{ x ≠ 0; x ≠ (-1/3); x ≠ (1/3)
{ D = 2^2 - 4(-1)*6 = 28 = (2sqrt(7))^2
x1 = (-2+2sqrt(7))/(-2) = 1 - sqrt(7) ≈ -1,65
x2 = (-2-2sqrt(7))/(-2) = 1 + sqrt(7) ≈ 3,65
x ∈ (1-sqrt(7); -1/3) U (-1/3; 0) U (0; 1/3) U (1/3; 1+sqrt(7))
Решаем уравнение:
(9x^2)^(1/2) = -x^2 + 2x + 6
Если x < 0, то (9x^2)^(1/2) = sqrt(9x^2) = -3x
-3x = -x^2 + 2x + 6
x^2 - 5x - 6 = 0
x1 = -1 - подходит по ОДЗ
x2 = 6 - не подходит по ОДЗ
Если x > 0, то (9x^2)^(1/2) = sqrt(9x^2) = 3x
3x = -x^2 + 2x + 6
x^2 + x - 6 = 0
x1 = 2 - подходит по ОДЗ
x2 = -3 - не подходит по ОДЗ
Ответ: x1 = -1; x2 = 2
12) log_4 (4^(-x) + 3) = x+1
ОДЗ:
4^(-x) + 3 > 0
Так как 4^(-x) > 0 при любом x, то:
x ∈ (-oo; +oo)
Решаем уравнение:
4^(x+1) = 4^(-x) + 3
4*4^x = 1/4^x + 3
Замена y = 4^x > 0 при любом x
4y = 1/y + 3
4y^2 = 3y + 1
4y^2 - 3y - 1 = 0
y1 = 1 > 0 - подходит
y2 = -1/4 < 0 - не подходит
y = 4^x = 1
Ответ: x = 0
13) lg(2 - x) = 2lg 4 - lg 2
lg - это десятичный логарифм, lg a = log_(10) a
ОДЗ:
2 - x > 0
x ∈ (-oo; 2)
Решаем уравнение.
lg(2 - x) = lg (4^2) - lg 2 = lg (16/2) = lg 8
2 - x = 8
x = 2 - 8 = -6 - подходит по ОДЗ
Ответ: x = -6
14) log_6 (6^(-x) + 5) = x - 1
Решается также, как 12)
ОДЗ:
x ∈ (-oo; +oo)
6^(x - 1) = 6^(-x) + 5
Замена y = 6^x, дальше сами.
15) log_5 (5^x - 4) = 1 - x
Это тоже решается также, как 12), но ОДЗ ограничено:
ОДЗ:
5^x - 4 > 0
x > log_5 4
x ∈ (log_5 4; +oo)
5^(1 - x) = 5^x - 4
Замена y = 5^x, дальше сами.
16) log_3 (2x+1) = log_3 13 + 1
ОДЗ:
2x + 1 > 0
x ∈ (-1/2; +oo)
log_3 (2x+1) = log_3 13 + log_3 3 = log_3 (13*3)
log_3 (2x+1) = log_3 39
2x + 1 = 39
x = 38/2 = 19
Ответ: x = 19
17) 2log_7 (x-2) = -2 + log_7 (x-10)^2
ОДЗ:
{ x > 2
{ x ≠ 10
x ∈ (2; 10) U (10; +oo)
2log_7 (x-2) = -2 + 2log_7 (x-10)
log_7 (x-2) = -1 + log_7 (x-10) = log_7 (1/7) + log_7 (x-10)
log_7 (x-2) = log_7((x-10)/7)
x - 2 = (x - 10)/7
7x - 14 = x - 10
6x = 4
x = 4/6 = 2/3 < 2 - не подходит по ОДЗ.
Ответ: Корней нет.
18) log_7 (7^(-x) + 6) = 1 + x
Это опять решается также, как 12)
ОДЗ:
x ∈ (-oo; +oo)
7^(1+x) = 7^(-x) + 6
Замена y = 7^x, дальше сами.
19) log_2 (2^x - 7) = 3 - x
Это решается, как 15), ОДЗ ограничен.
ОДЗ:
2^x - 7 > 0
x ∈ (log_2 7; +oo)
2^(3 - x) = 2^x - 7
Замена y = 2^x, дальше сами.
20) log_(x-3) (x^2 - 4x)^2 = 4
ОДЗ:
{ x-3 > 0; x-3 ≠ 1
{ x^2 - 4x ≠ 0
x ∈ (3; 4) U (4; +oo)
2log_(x-3) (x^2 - 4x) = 4
log_(x-3) (x^2 - 4x) = 2
(x-3)^2 = x^2 - 4x
x^2 - 6x + 9 = x^2 - 4x
9 = 6x - 4x
x = 9/2 - подходит по ОДЗ
Ответ: x = 9/2
Все решения
(x^2+x-6)^2-(x+1)^4=0
((x^2+x-6)-(x+1)^2)*((x^2+x-6)+(x+1)^2)=0
((x^2+x-6-x^2-2x-1)*(x^2+x-6+x^2+2x+1)=0
(-x-7)*(2x^2+3x-5)=0
-x-7=0 или 2x^2+3x-5=0
x_(1)=-7
или 2x^2+3x-5=0
D=9+40=49;
x_(2)=(-3-7)/4; x_(3)=(-3+7)/4
x_(2)=-5 x_(3)=1
Проверка:
x_(1)=-7 не является корнем, так как основание (х+1)=-7+1=-6 не может быть отрицательным числом
x_(2)=-5 не является корнем, так как основание (х+1)=-5+1=-4 не может быть отрицательным числом
О т в е т. х=1
Можно найти ОДЗ
ОДЗ:
{x^2+x-6)^2>0 ⇒ x^2+x-6 ≠ 0 ⇒ x ≠ -3; x ≠ 2
x+1>0 ⇒ x>-1
x+1 ≠ 1 ⇒ x ≠ 0
О т в е т. х=1