Задача 65128 Вычислить объем тела, ограниченного...
Условие
x^2 + y^2 = 9/2 ; x + y + z = 3 ; z = 0.
Решение
и неограниченный сверху.
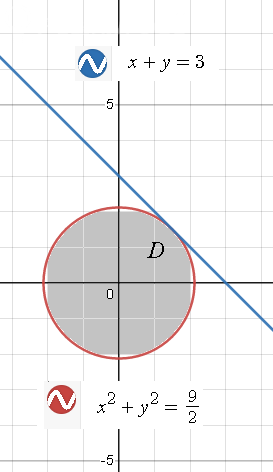
x+y+z=3 - плоскость, ограничивает тело сверху
[m]V= ∫ ∫_{D} (3-x-y)dxdy[/m]
D:
x^2+y^2 ≤ 9/2
Переходим к полярным координатам
[m]V= ∫ ∫_{D} (3- ρ cos φ - ρ sin φ ) ρ d ρ d φ= ∫_{0}^{2π} ( ∫_{0}^{\sqrt{\frac{9}{2}}} (3 ρ - ρ^2 cos φ - ρ^2 sin φ)d ρ)d φ = [/m]
[m]=∫_{0}^{2π} ( 3 \frac{ ρ ^2}{2}-cos φ \frac{ ρ ^3}{3}-sin φ \frac{ ρ ^3}{3}) |_{0}^{\sqrt{\frac{9}{2}}} )d φ =[/m]
[m]=∫_{0}^{2π} (3\cdot \frac{9}{4}-\frac{(\sqrt{\frac{9}{2}})^3}{3}cos φ -\frac{(\sqrt{\frac{9}{2}})^3}{3}sin φ)d φ =...[/m]