Задача 65064 Решить y’=(x/y)+(y/x)...
Условие
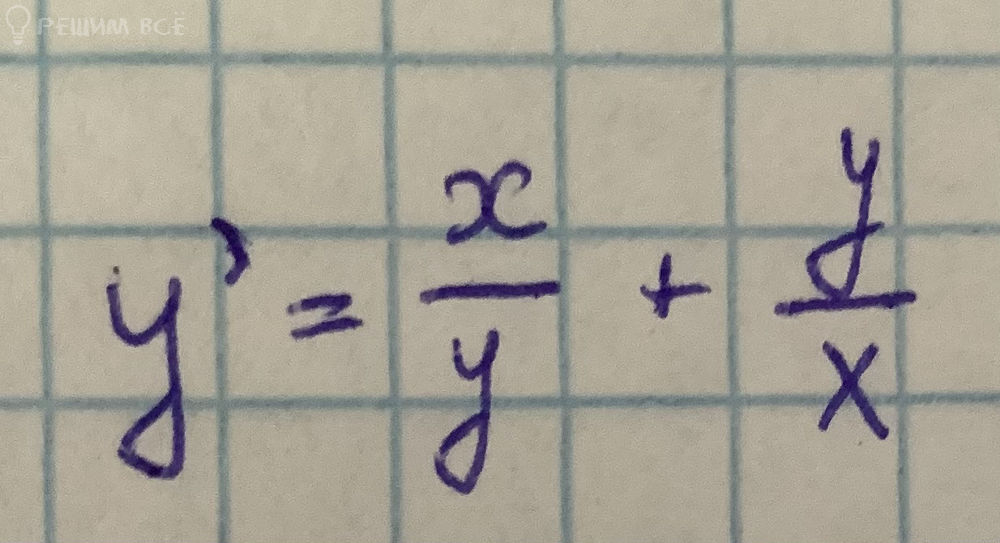
80
Решение
★
Решается заменой
y/x=u
y=u*x
y`=u`*x+u*x`
x`=1 ( так как x - независимая переменная)
y`=u`*x+u
Подставляем в уравнение:
u`*x+u=(1/u)+u
u`*x=(1/u) - уравнение с разделяющимися переменными
u`=du/dx
x*du=(1/u)dx
u*du=(1/x)dx
Интегрируем:
∫ u*du= ∫ (1/x)dx
u^2/2=ln|x| +lnс
u^2=2lnx+2lnс
u^2=lnс^2x^2
e^(u^2)=с^2x^2
Обратный переход к переменным х и у
e^((y/x)^2)=с^2x^2
с^2 можно заменить на С
e^((y/x)^2)=Cx^2