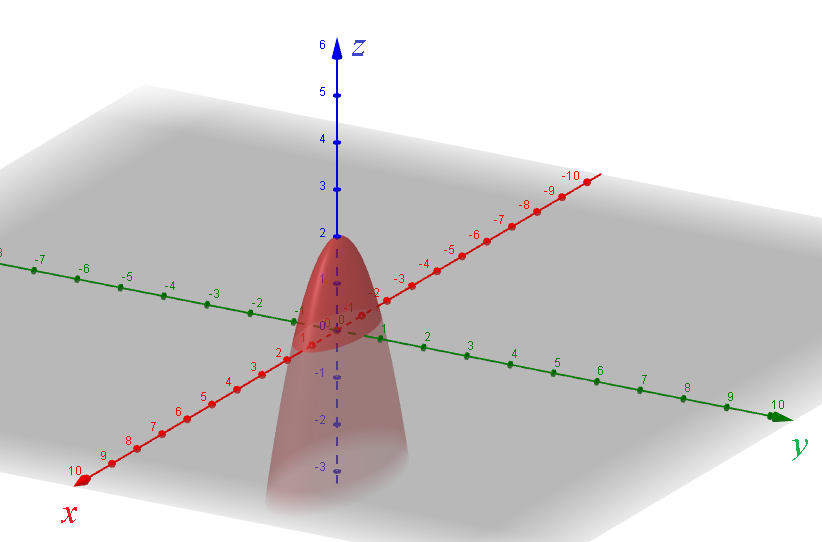
Задача 64951 Сделать чертеж области, ограниченной...
Условие
Вычислить площадь полученной фигуры.
Решение
Где [m]S(z) [/m]- площадь сечения плоскостями, параллельными плоскости хОу
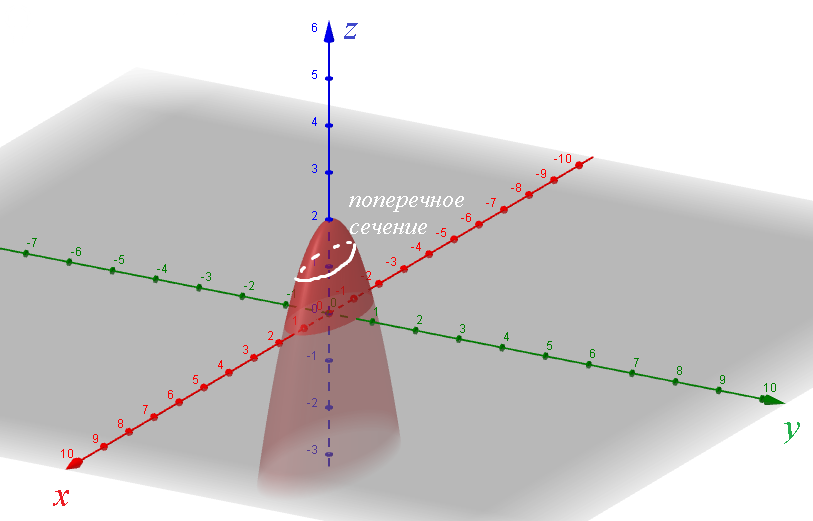
В сечениях получатся[b] эллипсы:[/b] ( см. рис.)
{z=2-x^2-5y^2
{z=0
⇒
x^2+5y^2=2 - область D на плоскости xOy
z=2 - наибольшее значение по оси Оz
Пересекаем тело плоскостями
z=h,
0 ≤ h ≤ 2
{z=2-x^2-5y^2
{z=h, 0 ≤ h ≤ 2 ⇒
x^2+5y^2=2-h
Это уравнение эллипса
x^2/(2-h) + y^2/(2-h)/5 =1
a^2=2-h
b^2=(2-h)/5
S_(эллипса)=π*a*b
S_(h)=π*\sqrt(2-h)*sqrt((2-h)/5)
S(z)=π*\sqrt(2-z)*sqrt((2-z)/5)
V= ∫_(0)^(2) S_(z) dz=∫_(0)^(2) π (2-z)/sqrt(5)dz=π/(sqrt(5))∫_(0)^(2)(2-z)dz=π/(sqrt(5))*(2z-(z^2/2))|_(0)^(2)=π/(sqrt(5))*(2*2-(2^2/2))=2π/(sqrt(5))=[b]2πsqrt(5)/5[/b]