Задача 64902 ...
Условие
1) √(3x + 1) = 6
2) √(x^2 - 3) = 7
3) √(4x - 5) = 2x
4) √(x - 9) = √(1-x)
5) √(x^2 + 3x + 5) = 3
6) √x = x-6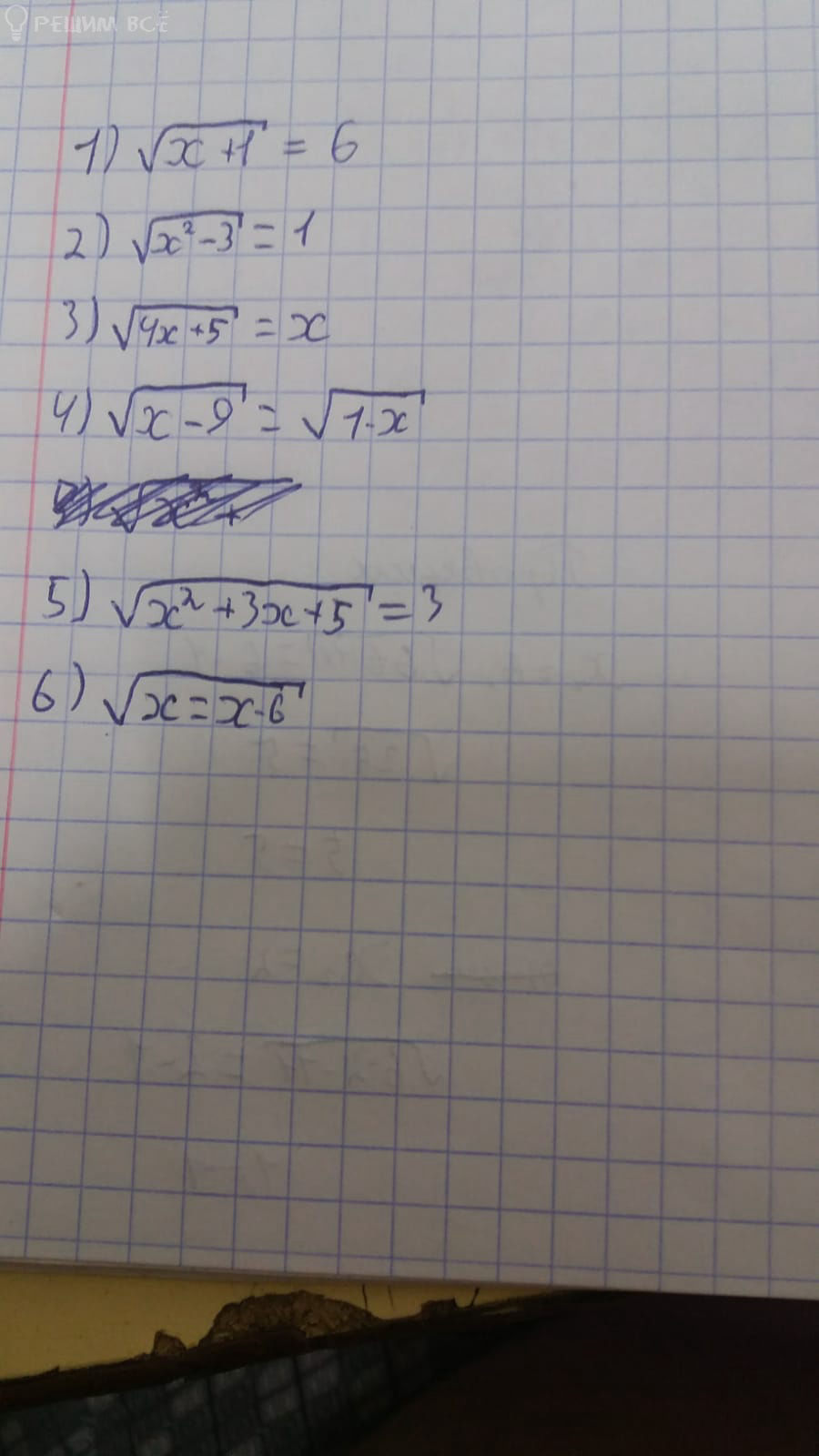
Решение
Выражение под корнем и сам корень должны быть неотрицательными.
1) Если корень равен просто числу, то область определения можно не определять.
x+1 = 36
x = 35
2) x^2 - 3 = 1
x^2 = 4
x1 = -2; x2 = 2
3) Так как корень арифметический, то есть неотрицательный, то область определения:
{ 4x + 5 ≥ 0
{ x ≥ 0
4x + 5 = x^2
x^2 - 4x - 5 = 0
(x - 5)(x + 1) = 0
x = -1 не подходит
x = 5
4) Область определения:
{ x ≥ 9
{ x ≤ 1
Это противоречие, поэтому корней нет.
5) Область определения:
x^2 + 3x + 5 ≥ 0
D = 3^2 - 4*1*5 = -11 < 0
x € (-oo; +oo)
x^2 + 3x + 5 = 9
x^2 + 3x - 4 = 0
(x- 1)(x + 4) = 0
x1 = -4; x2 = 1
6) Неправильно написано.
Знак = не может быть под корнем