Задача 64644 ...
Условие
Σ arctg^2 n / n^3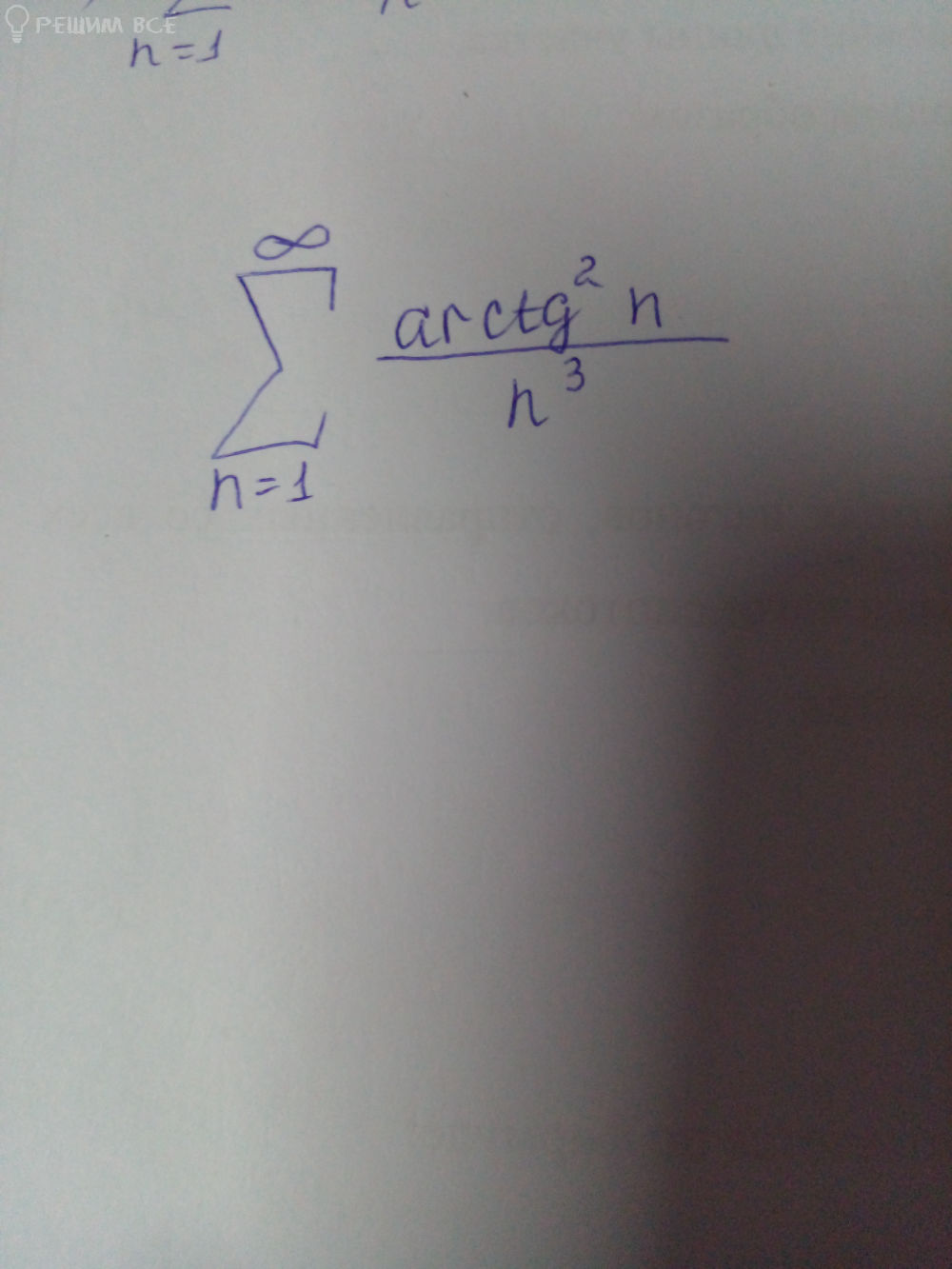
математика ВУЗ
266
Решение
★
Так как
[m] \frac{π}{2} ≤ arctgx ≤ \frac{π}{2}[/m] при любых x
[m]a_{n}=\frac{arctg^2n}{n^3} ≤ \frac{(\frac{π}{2})^2}{n^3}[/m]
a ряд ∑ _(n=1)^( ∞ )[m]\frac{1}{n^3}[/m] cходится.
Обобщенный гармонический ряд ∑ _(n=1)^( ∞ )[m]\frac{1}{n^{ α} }[/m] cходится при [b]α >1[/b]
Или по интегральному признаку, так как сходится интеграл [m] ∫ _{1}^{ ∞ }\frac{1}{x^{ 3} }dx=∫ _{1}^{ ∞ }x^{- 3}dx=(\frac{x^{-2}}{-2})|_{1}^{ ∞ }=0-(-\frac{1}{2})[/m]