Задача 64350 Нужно найти площадь фигуры, ограниченную...

6183f5e0f87a077765ec8006

01.05.2022 20:22:06

Нужно найти площадь фигуры, ограниченную линию

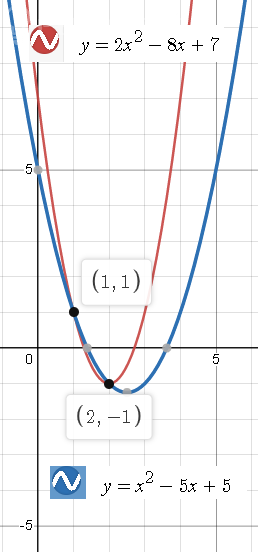
y = 2x^2 - 8x + 7, y = x^2 - 5x + 5;

5f3ea7e3faf909182968ddd9

01.05.2022 23:05:27

★

Находим абсциссы точек пересечения графиков:

2x^2-8x+7=x^2-5x+5

x^2-3x+2=0

x_(1)=1; x_(2)=2

Строим графики. См. рис.

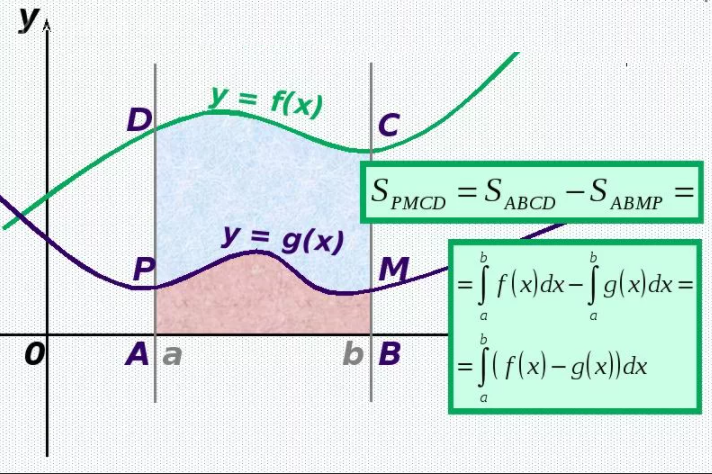
По правилу ( см. скрин):


[m]S= ∫_{1}^{2} ((x^2-5x+5)-(2x^2-8x+7))dx=∫_{1}^{2}(-x^2+3x-2)dx=(-\frac{x^3}{3}+3\frac{x^2}{2}-2x)|_{1}^{2}=[/m]

[m]=(-\frac{2^3}{3}+3\frac{2^2}{2}-2\cdot 2)-(-\frac{1^3}{3}+3\frac{1^2}{2}-2\cdot 1)=...[/m]