Задача 63981 e o7 Log, 2y bl * Lag ...
Условие
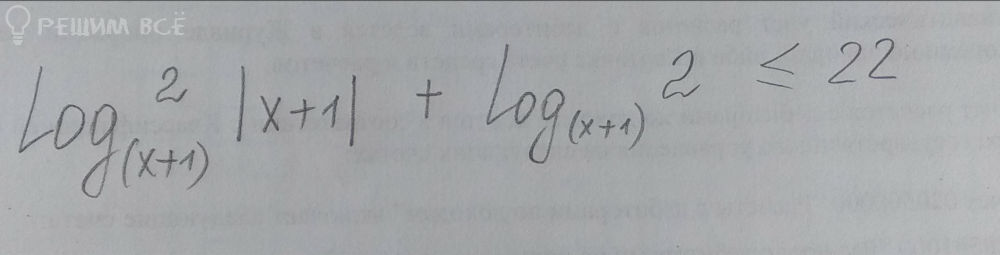
Решение
[m]\left\{\begin {matrix}x+1>0\\x+1 ≠1\\|x+1|>0 \end {matrix}\right.[/m] ⇒ [m]\left\{\begin {matrix}x>-1\\x ≠0\\x ≠- 1 \end {matrix}\right.[/m] ⇒[red] [m]x ∈ (-1;0)\cup(0;+ ∞ )[/m][/red]
Раскрываем модуль по определению:
1) если [m]x+1 ≥ 0[/m] ⇒[blue] [m]x ≥ -1[/m] [/blue]
[m]|x+1|=x+1[/m]
Неравенство
[m]log^2_{x+1}(x+1)+log_{x+1}2 ≤ 22[/m]
Так как
[m]log_{x+1}(x+1)=1[/m]
[blue][m]1^2+log_{x+1}2 ≤ 22[/m][/blue]
[m]log_{x+1}2 ≤ 21[/m] ⇒ [m]log_{x+1}2 ≤ 21\cdot log_{x+1}(x+1)[/m]⇒ [m]log_{x+1}2 ≤ log_{x+1}(x+1)^{21}[/m]
если 0< x+1 < 1, то [m] y=log_{x+1}t [/m]убывающая
2 ≥ (x+1)^{21} ⇒ x+1 ≤ \sqrt[21]{2} ⇒ x ≤ \sqrt[21]{2}-1
Из неравенств
0< x+1 < 1 и x ≤ \sqrt[21]{2}-1
решением является [b] -1 < x <0 [/b]
если x+1> 1, то [m] y=log_{x+1}t [/m]возрастающая
2 ≤ (x+1)^{21} ⇒ x+1 ≥ \sqrt[21]{2} ⇒ x ≥ \sqrt[21]{2}-1
x+1> 1 и x ≥ \sqrt[21]{2}-1
решением является [b] x ≥ \sqrt[21]{2}-1[/b]
Оба решения входят в ОДЗ
2)
если
[m]x+1 < 0[/m] . то x <-1 а это не удовлетворяет ОДЗ
О т в е т. [b] -1 < x <0[/b] или [b] x ≥ \sqrt[21]{2}-1[/b]