Задача 63762 1. Найти частные производные от функций...
Условие
математика колледж
131
Решение
★
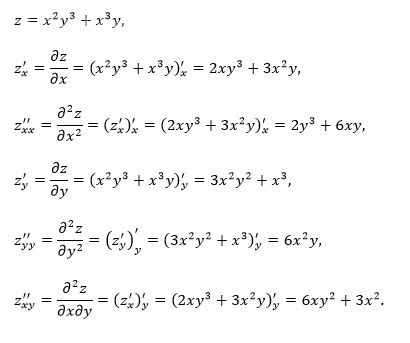
Все решения
[m]\frac{ ∂u }{ ∂x }=z`_{x}=(x^2y^3+x^3y)`_{x}=y^3\cdot (x^2)`+y\cdot (x^3)`=y^3\cdot 2x+y\cdot 3x^2=2xy^3+3x^2y[/m]
[m]\frac{ ∂u }{ ∂y }=z`_{y}=(x^2y^3+x^3y)`_{y}=x^2\cdot (y^3)`+x^3\cdot (y)`=x^2\cdot 3y^2+x^3\cdot1=3x^2y^2+x^3[/m]