Задача 63754 ...

6197826fc30ab457e8749ac7

23.03.2022 11:47:58

Случайная величина X задана функцией распределения F(x). Вычислить вероятность попадания случайной величины X в заданный интервал. Найти плотность распределения случайной величины X. Построить графики f(x) и F(x).

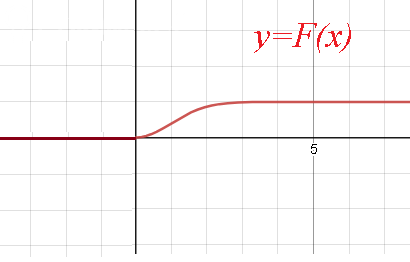
F(x) =
{ 0, x ≤ 0
{ 1-e^(-x^2/2), x > 0


(√2; 2)

5f3ea7e3faf909182968ddd9

23.03.2022 17:49:38

★

Так как [m]f(x)=F `(x)[/m]

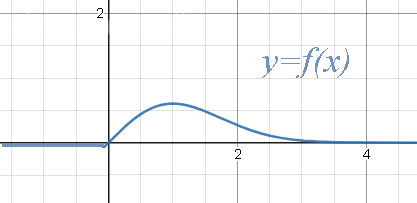
[m]f(x)=\left\{\begin{matrix}
0,если x ≤ 0\\-e^{-\frac{x^2}{2}}\cdot(-\frac{x^2}{2})` , если x > 0\end{matrix}\right.[/m] ⇒

[m]f(x)=\left\{\begin{matrix}
0,если x ≤ 0\\x \cdot e^{-\frac{x^2}{2}} , если x > 0\end{matrix}\right.[/m]


[m]P(-\sqrt{2}<X<2)=F(2)-F(-\sqrt{2})=1-e^{-\frac{2^2}{2}}-(1-e^{-\frac{(\sqrt{2})^2}{2}})=e^{-1}-e^{-2}[/m]