Задача 63616 Задана плотность распределения...
Условие
а) Найдите функцию распределения F(x)
б) Найдите вероятность того, что величина X примет значение из промежутка [3; 4]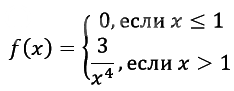
Решение
Так как функция задана на двух промежутках, то
[m]∫ ^{+ ∞ }_{- ∞}f(x)dx=∫ ^{1 }_{- ∞}0dx+∫ ^{+ ∞ }_{1}\frac{3}{x^4}dx[/m]
По определению:
[m]F(x)= ∫ ^{x}_{- ∞ }f(x)dx[/m]
[b]При x ≤1[/b]
[m]F(x)= ∫ ^{x}_{- ∞ }0dx=0[/m]
[b]При x > 1[/b]
[m]F(x)= ∫ ^{x}_{- ∞ }f(x)dx=[/m]
Так как функция [m]f(x)[/m] задана на двух промежутках, то
[m]=∫ ^{1}_{- ∞ }0dx+∫ ^{x}_{1}\frac{3}{x^4}dx=3∫ ^{x}_{1}x^{-4}dx=3(\frac{x^{-3}}{(-3)})|^{x}_{1}=-\frac{1}{x^3}+1=1-\frac{1}{x^3}[/m]
Получаем:
[m]F(x)\left\{\begin {matrix}0, x ≤1\\1-\frac{1}{x^3}, x > 1 \end {matrix}\right.[/m]
По формуле:
[m]P( α ≤ x ≤ β )=F( β )-F( α )[/m]
получаем:
[m]P( 3 ≤ x ≤ 4 )=F(3 )-F(2)=(1-\frac{1}{4^3})-(1-\frac{1}{3^3})=\frac{1}{27}-\frac{1}{64}=...[/m]
считайте