Задача 63608 ...
Условие
∑ (n=2 to ∞) (sqrt(ln(n + 1))/(n + 1)) * x^(n)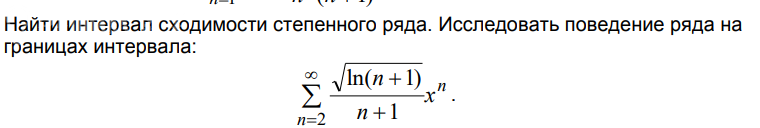
математика ВУЗ
201
Решение
★
(-1;1) - интервал сходимости ряда
При x=-1
получаем знакочередующийся числовой ряд [m] ∑_{2} ^{ ∞ }\frac{\sqrt{ln(n+1)}}{n+1} (-1)^{n} [/m]
Исследуем его на сходимость
При x=1
получаем знакоположительный числовой ряд [m] ∑_{2} ^{ ∞ }\frac{\sqrt{ln(n+1)}}{n+1} (1)^{n} [/m]
Исследуем его на сходимость