Задача 63553 ...
Условие
∑ (n=1 to ∞) (cos² n) / ((n + 2) ln^2(n + 3))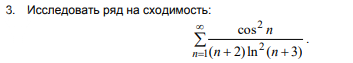
математика ВУЗ
335
Решение
★
Применяем признак Абеля ( см. скрин1)
1)
Последовательность (a_(n))
a_(n)=cos^2n ограничена, так как 0 ≤ cos^2n ≤ 1
2)
Ряд[m]∑_{1}^{+ ∞}\frac{1}{(n+2)ln^2(n+3)} [/m]- сходится ( cм. признак сравнения), так как [i]эквивалентен[/i] ряду [m]∑_{1}^{+ ∞}\frac{1}{(n+3)ln^2(n+3)} [/m], который сходится по интегральному признаку
[m] ∫_{1}^{+ ∞} \frac{dx}{(x+3)ln^2(x+3)}=∫_{1}^{+ ∞} \frac{d(ln(x+3)}{ln^2(x+3)}=-\frac{1}{ln(x+3)}|_{1}^{+ ∞}=0+\frac{1}{ln4}[/m],
О т в е т. Ряд сходится по признаку Абеля