Задача 63337 ...
Условие
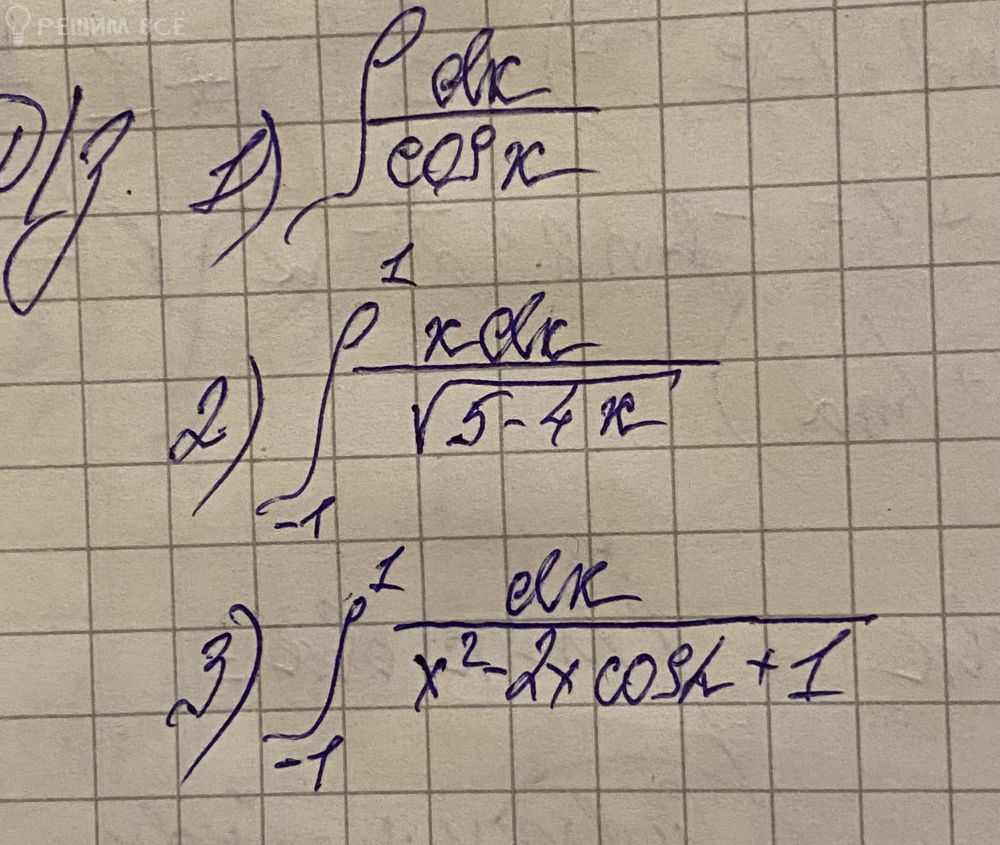
математика ВУЗ
530
Решение
★
[m] ∫_{-1} ^{1}\frac{xdx}{\sqrt{5-4x}}=[/m]
замена переменной:
[m]\sqrt{5-4x}=t[/m] ⇒ [m]5-4x=t^2[/m] ⇒ [m]x=-\frac{t^2-5}{4}[/m]
[m]dx=-2tdt[/m]
тогда
[m]∫\frac{xdx}{\sqrt{5-4x}}= ∫(- \frac{t^2-5}{4t})(-2tdt)= ∫\frac{t^2-5}{2}dt=\frac{1}{2}∫(t^2-5)dt=\frac{1}{2}\cdot (\frac{t^3}{3}-5t)+C=\frac{t^3}{6}-\frac{5}{2}t+C=\frac{(\sqrt{5-4x})^3}{6}-\frac{5}{2}\sqrt{5-4x}+C [/m]
Тогда
[m] ∫_{-1} ^{1}\frac{xdx}{\sqrt{5-4x}}=(\frac{(\sqrt{5-4x})^3}{6}-\frac{5}{2}\sqrt{5-4x})|_{-1} ^{1}=-frac{7}{12}-(-\frac{3}{4}= [/m] считайте...
1)
