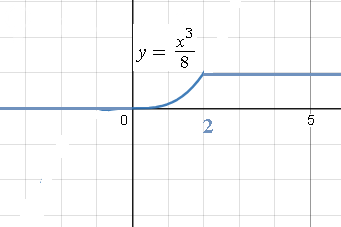Задача 63274 найти и построить......
Условие
математика ВУЗ
217
Решение
★
[m]F(x)= ∫ ^{x}_{- ∞ }f(x)dx[/m]
[b]При x ≤0[/b]
[m]F(x)= ∫ ^{x}_{- ∞ }0dx=0[/m]
[b]При 0 < x ≤ 2[/b]
[m]F(x)= ∫ ^{x}_{- ∞ }f(x)dx=∫ ^{0}_{- ∞ }0dx+∫ ^{x}_{0}\frac{3x^2}{8}dx=3(\frac{x^3}{8\cdot 3})^{x}_{0}=(\frac{x^3}{8})^{x}_{0}=\frac{x^3}{8}[/m]
При x > 2
[m]F(x)= ∫ ^{x}_{- ∞ }f(x)dx=∫ ^{0}_{- ∞ }0dx+∫ ^{2}_{0}\frac{3x^2}{8}dx+∫ ^{x}_{2}0dx=(\frac{x^3}{8})|^{2}_{0}=11[/m]
[m]F(x)\left\{\begin {matrix}0, x ≤ 0\\\frac{x^3}{8},0 < x ≤2\\1, x > 2 \end {matrix}\right.[/m]
