Задача 62889 ...

61f10f7f31fd593948de84a8

27.01.2022 16:27:10

Случайная величина X задана функцией распределения F(x). Вычислить вероятность попадания случайной величины X в заданный интервал. Найти плотность распределения случайной величины X. Построить графики f(x) и F(x).

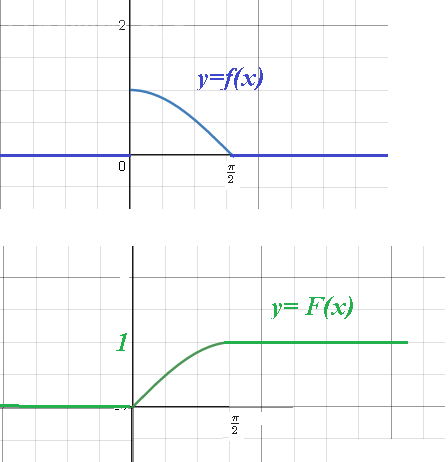
F(x) =
{ 0, x ≤ 0
{ sin x, 0 < x ≤ π/2
{ 1, x > π/2


(π/4, π/3)

5f3ea7e3faf909182968ddd9

27.01.2022 16:43:39

★

Так как [m]f(x)=F `(x)[/m]

[m]f(x)=\left\{\begin{matrix}
0,если x ≤ 0\\cosx, если 0<x≤ \frac{π}{2}\\0, если x >\frac{π}{2} \end{matrix}\right.[/m]

По формуле:

[m]P( α ≤ x ≤ β )=F( β )-F( α )[/m]

получаем:

[m]P( \frac{π}{4} < x <\frac{π}{3} )=F(\frac{π}{3} )-F(\frac{π}{4})=sin\frac{π}{3}-sin\frac{π}{4}=\frac{\sqrt{3}}{2}-\frac{\sqrt{2}}{2}=\frac{\sqrt{3}-\sqrt{2}}{2}[/m]