Задача 627 В правильной шестиугольной призме...
Условие
математика 10-11 класс
27548
Решение
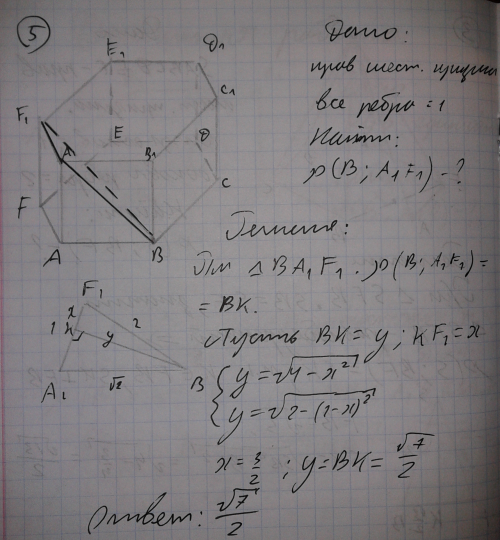
Ответ: sqrt(7)/2

Ответ: sqrt(7)/2