Задача 62386 ...
Условие
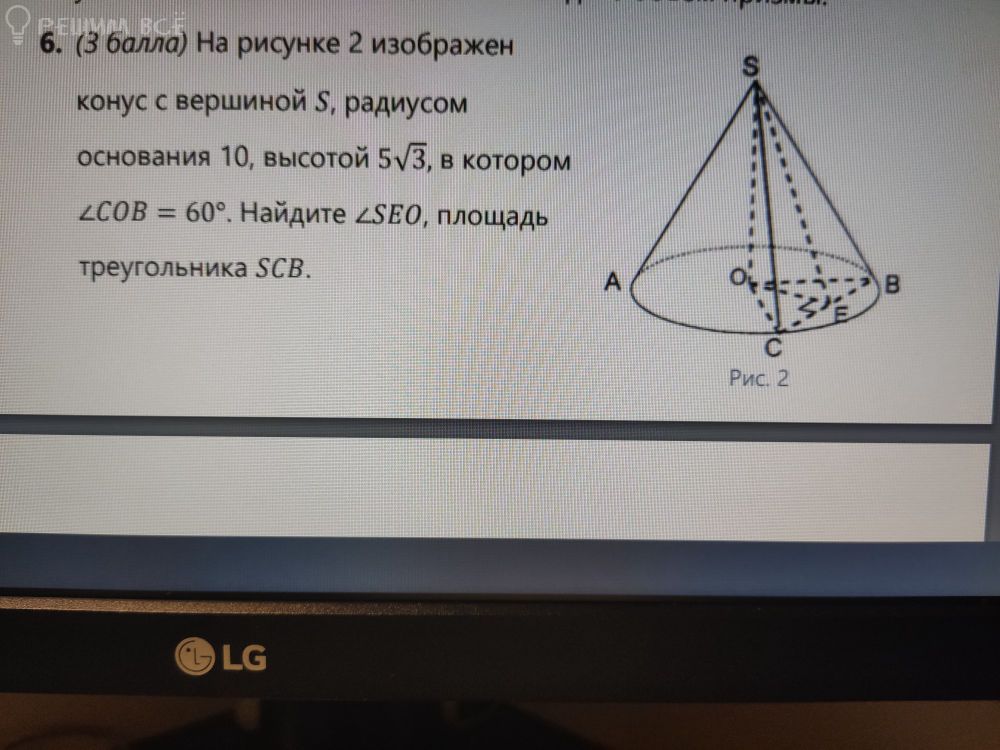
математика 10-11 класс
271
Решение
★
BC=OC=OB=R=10
OE=10*sin60 ° =5sqrt(3)
tg ∠ SEO=SO/OE=1
∠ SEO=45 °
SE=OE/cos45 ° =10sqrt(3)/sqrt(2)=10 sqrt((3/2))
S_( ΔSBE)=(1/2)BC*SE=(1/2)*10*(10 sqrt((3/2))=50 sqrt(3/2)=[b]25sqrt(6)[/b]