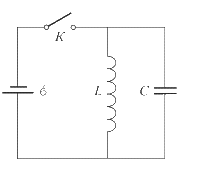
Задача 618 Колебательный контур через ключ К...

slava191

14.02.2014

Колебательный контур через ключ К подключен к источнику ЭДО с некоторым внутренним сопротивлением r (см. рисунок). Первоначально ключ К замкнут. После установления
стационарного режима ключ размыкают и в контуре возникают колебания с периодом Т. При этом амплитуда напряжения на конденсаторе в п раз больше ЭДС батареи. Определите индуктивность L катушки и емкость С конденсатора. Активное сопротивление контура пренебрежимо мало.

Что Вы можете сделать?

1. Выставите данный вопрос вновь. Перейдите на главную страницу.
2. Найдите похожую задачу. Используйте поиск.