Задача 61796 Найти углы,под которыми пересекаются...
Условие

Решение
Решаем систему уравнений:
{x^2=y
{x^2=3-2y^2
Приравниваем правые части
y=3-2y^2
2y^2+y-3=0
D=1-4*2*(-3)=25
y_(1)=-3/2; y_(2)=1
x^2=-3/2 - уравнение не имеет решений
x^2=1 ⇒ x_(1)=-1; x_(2)=1
Составить уравнения касательных к каждой кривой в точках x_(1)=-1; x_(2)=1
y-f(x_(o))=f`(x_(o))*(x-x_(o))
1)
y=x^2
Точка [b]х=-1[/b]
f`(x)=2x
f`(-1)=2*(-1)=-2
y-1=-2*(x-(-1))
[b]y=-2x-1 [/b]
Точка [b]х=1[/b]
f`(1)=2*1=2
y-1=2*(x-1)
[b]y=2x-1[/b]
2)
x^2+2y^2=3
2x+4y*y`=0
y`=-2x/4y
[b]x=-1[/b] ; y=1
f`(-1)=-2*(-1)/4*(1)=1/2
y-1=(1/2)*(x-(-1))
[b]y=(1/2)x+(3/2) [/b]
Точка [b]х=1[/b] ; y=1
f`(1)=-2*1/4=-1/2
y-1=(-1/2)*(x-1)
[b]y=(-1/2)x+(3/2) [/b]
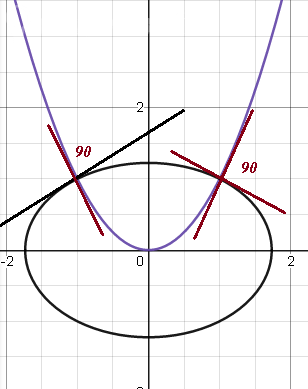
Угол между касательными в точке х=-1, т.е между прямыми [b]y=[red]-2[/red]x-1 [/b] и [b]y=[red](1/2)[/red]x+(3/2) [/b] равен 90 ° ,так как произведение угловых коэффициентов равно (-1)
Угол между касательными в точке х=1, т.е между прямыми [b]y=[red]2[/red]x-1 [/b] и [b]y=[red](-1/2)[/red]x+(3/2) [/b] равен 90 °,так как произведение угловых коэффициентов равно (-1)