Задача 61473 ...
Условие
∑_(n=1)^(∞) (1/(3^n)) ((n/(n+1))^(-n^2))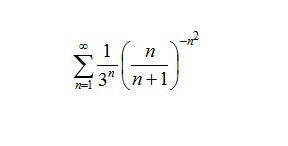
математика
244
Решение
★
[m]lim_{n → ∞ }\sqrt[n]{a_{n}}=lim_{n → ∞ }\sqrt[n]{\frac{1}{3^{n}}\cdot (\frac{n}{n+1})^{-n^2}}=lim_{n → ∞ }\frac{1}{3}\cdot (\frac{n}{n+1})^{-n}=\frac{1}{3}lim_{n → ∞ }(\frac{n+1}{n})^{n}=\frac{e}{3} < 1[/m]
Ряд сходится